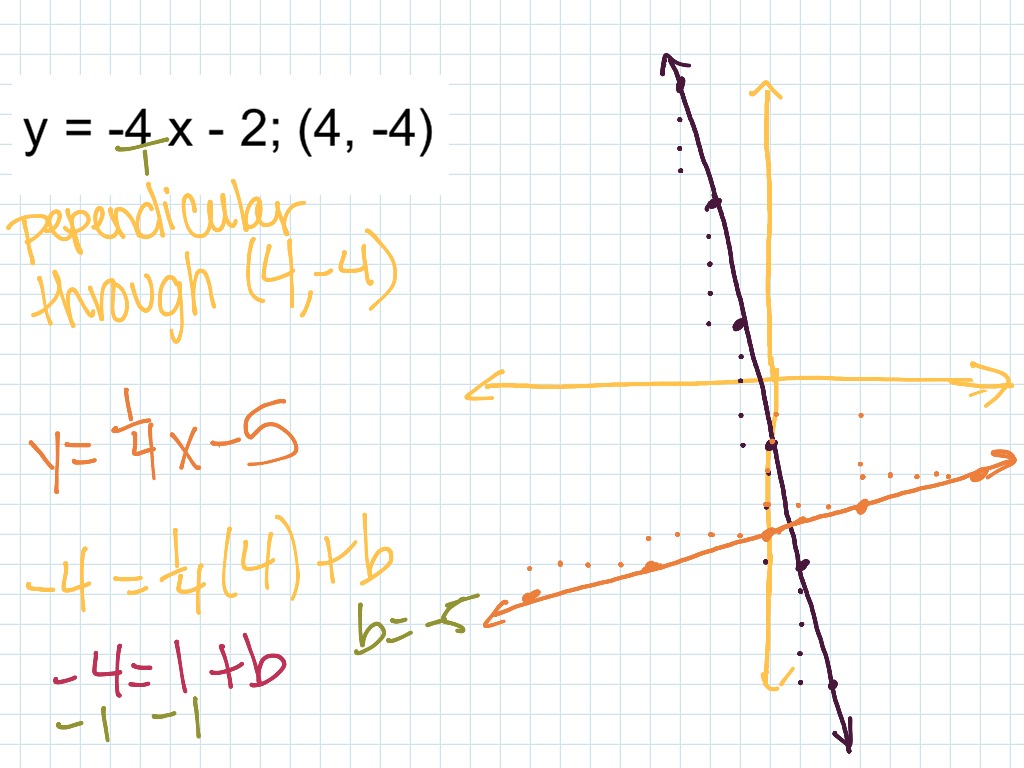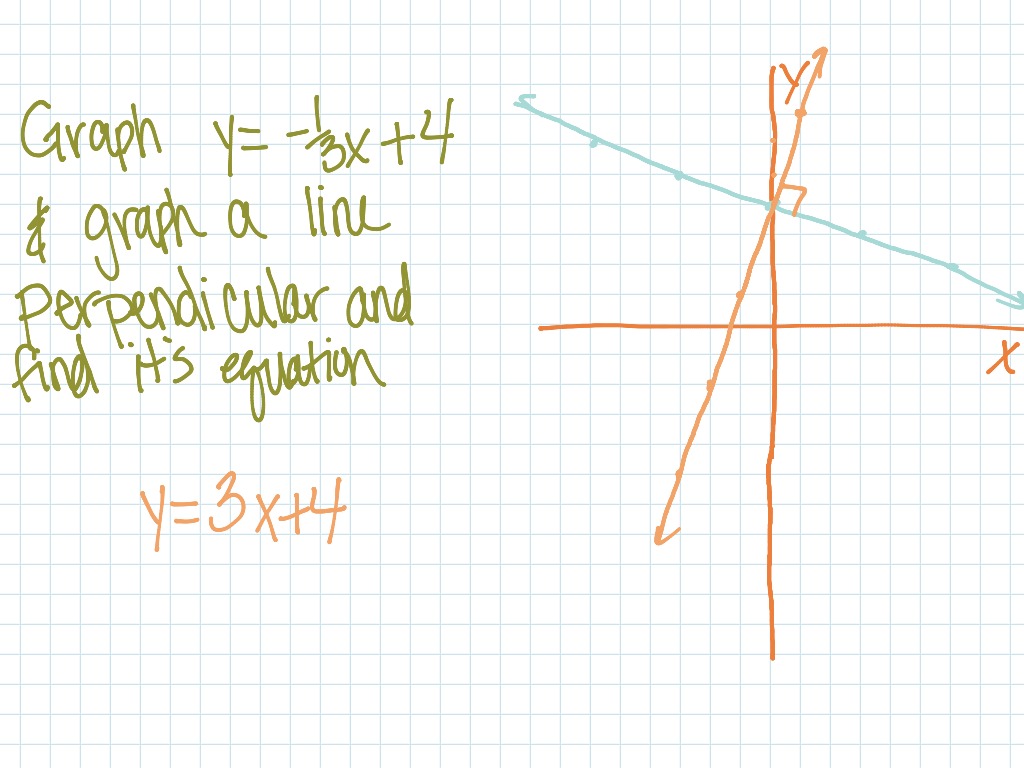Fantastic Info About Graphing Parallel And Perpendicular Lines Graph Line Online

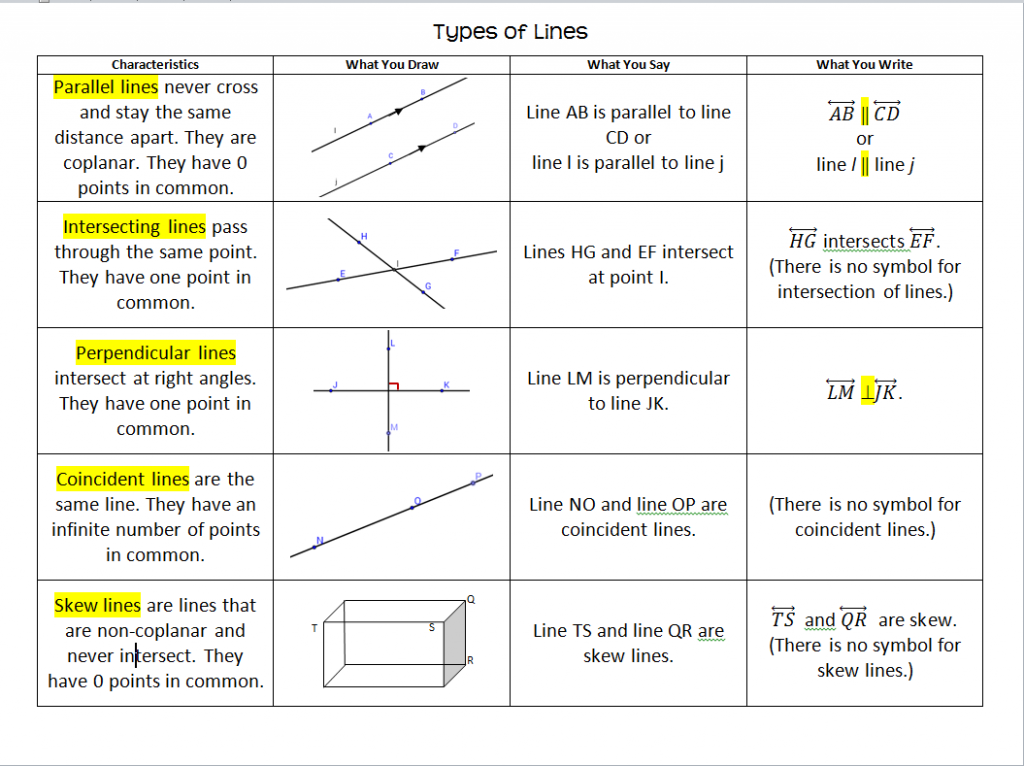
Developmental math (nroc) 13:

Graphing parallel and perpendicular lines. For example, 60° + 120° = 180°, so 60° and 120° are supplementary angles. Complementary angles are two angles that add up to 90°. Line b increases from left to right and passes through points negative seven, negative nine and three, negative two.

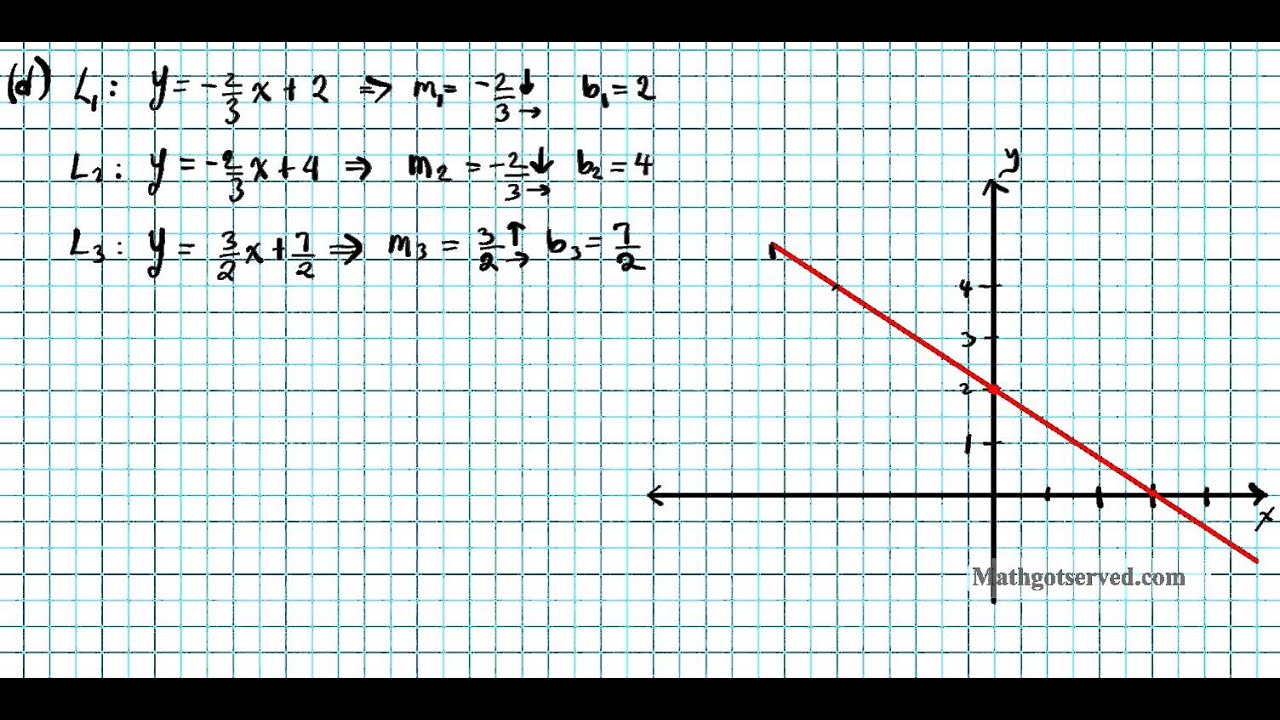
Let's expand 2 (x − 5) and then rearrange: Parallel lines have slopes that are the same. Lines that are perpendicular intersect to form a {90}^ {\circ } 90∘ angle.

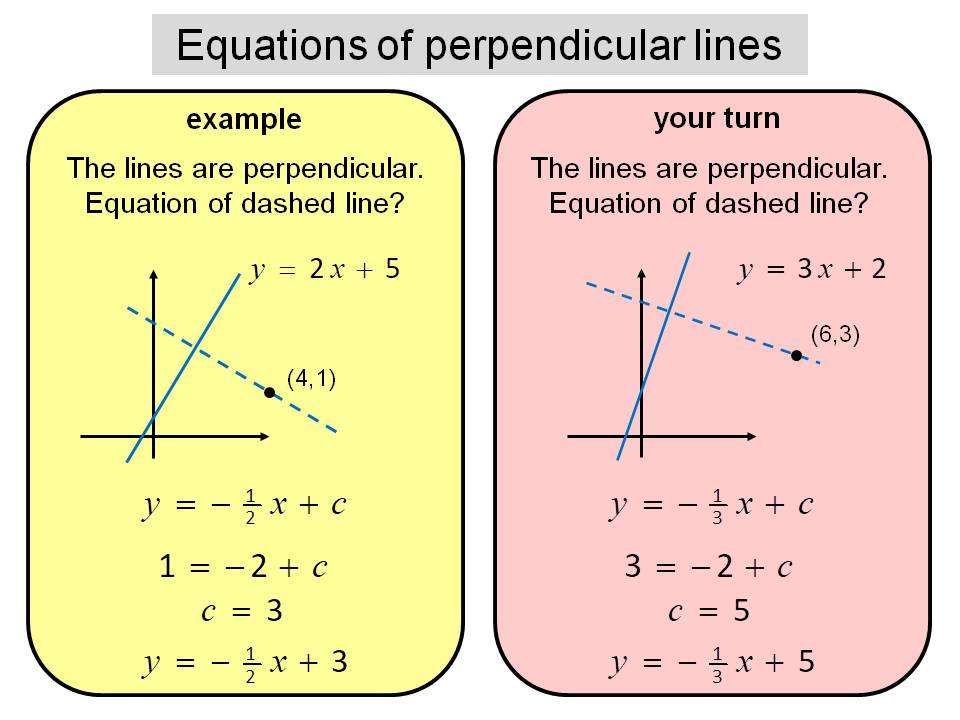
11 comments ( 188 votes) upvote downvote We can clearly see that the two lines have different y−intercepts: Finding equations of parallel and perpendicular lines.

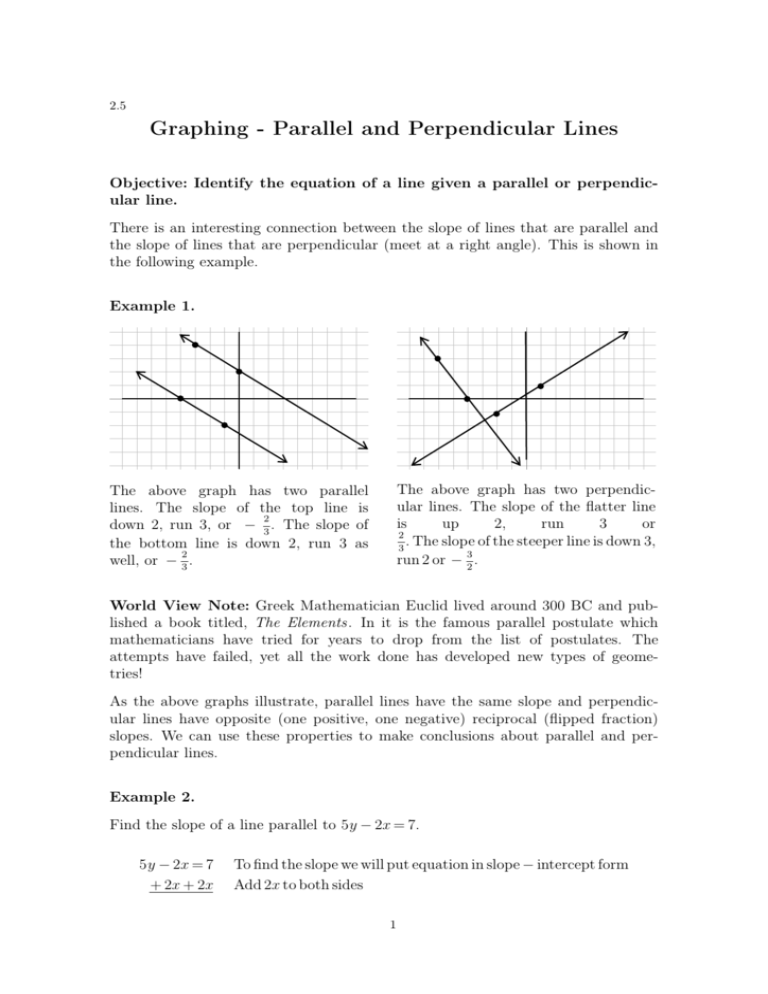
Lines that are parallel have the same slopes. Line a increases from left to right and passes through points two, five and seven, eight. Let’s start by looking at a graph of two parallel lines.

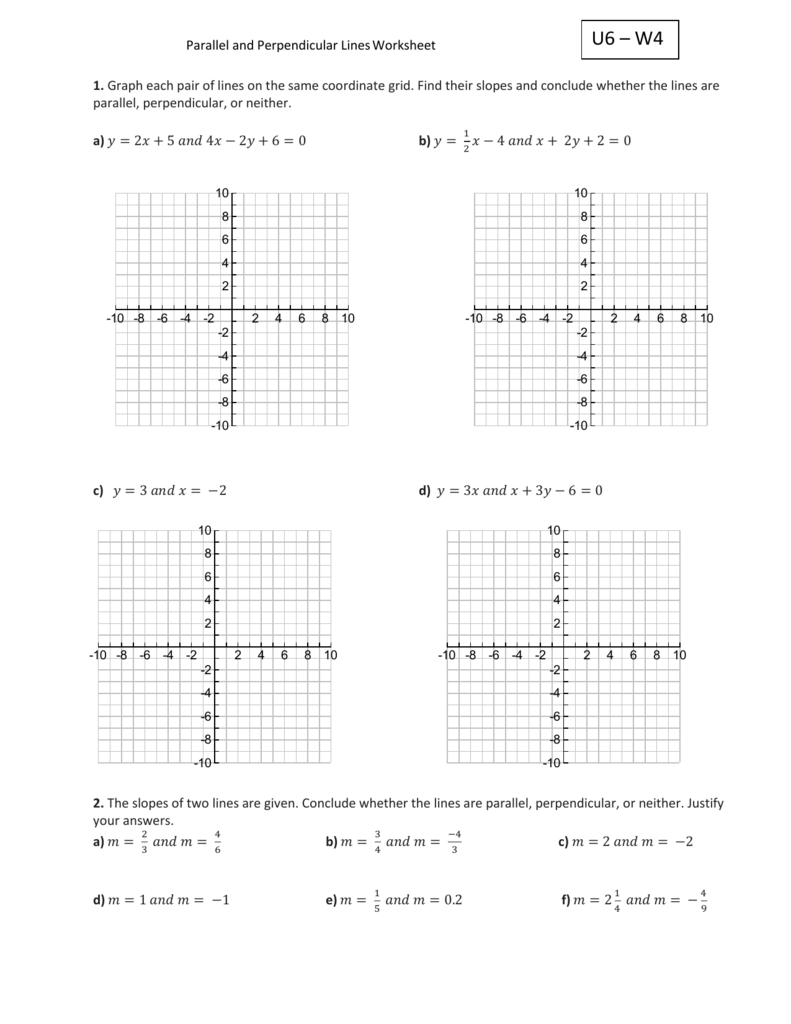
2.13.1 straight line graphs (y = mx + c) 2.13.2 parallel & perpendicular lines; Parallel lines questions answers. If you have the equation, you can graph it by hand by graphing the point and then counting the slope from there.

Often you will be asked to find the equation of a line given some geometric relationship—for instance, whether the line is parallel or perpendicular to another line. Revision notes on 2.13.2 parallel & perpendicular lines for the cie igcse maths: Parallel to \(x = 0\)

Multiplication practice questions the corbettmaths practice questions on parallel lines and perpendicular lines Find the slope of a line parallel to 5y − 2x = 7. Finding equations of parallel and perpendicular lines.

Now, we want to graph a line perpendicular to this line and passing through \((−2,1)\). Graphing parallel and perpendicular lines (kristakingmath) watch on. They're two angles that add up to 180°.

Extended syllabus, written by the maths experts at save my exams. Write the equations of lines that are parallel or perpendicular to a given line. In this section you will learn how parallel lines and perpendicular lines are related to each other on the coordinate plane.

We have seen that the graph of a line is completely determined by two points or one point and its slope. Often you will be asked to find the equation of a line given some geometric relationship—for instance, whether the line is parallel or perpendicular to another line. Lines that are parallel to each other will never intersect.