What Everybody Ought To Know About Is Conic A Parabola How Make Line Graph In Excel

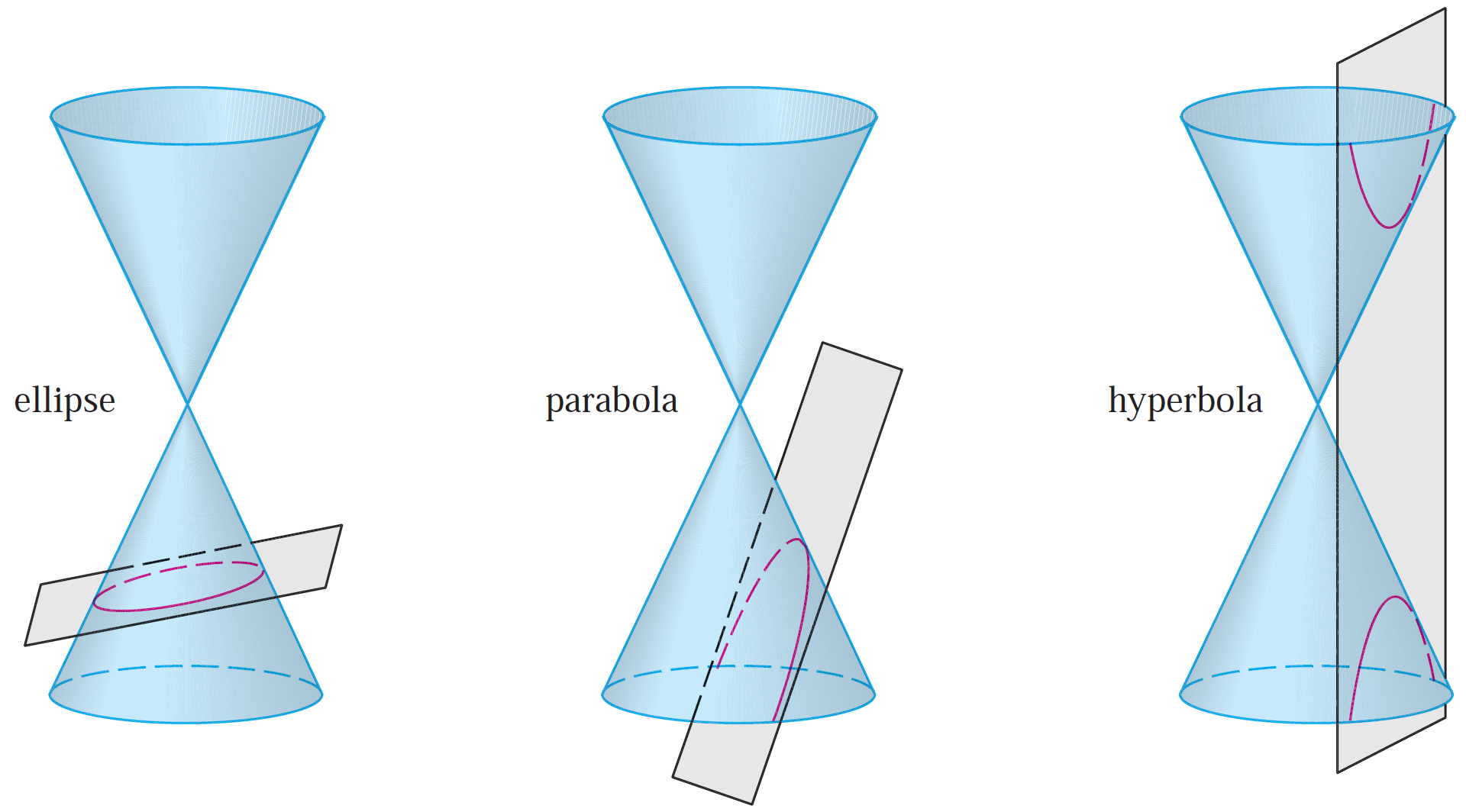
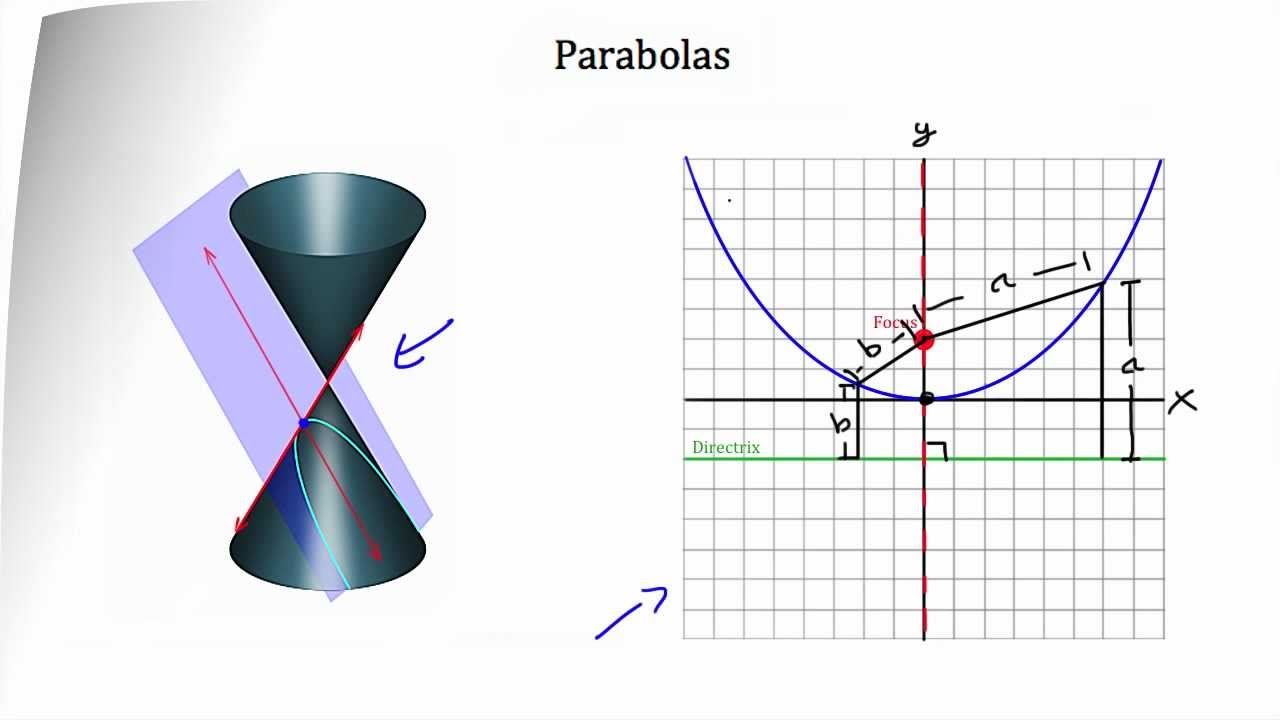
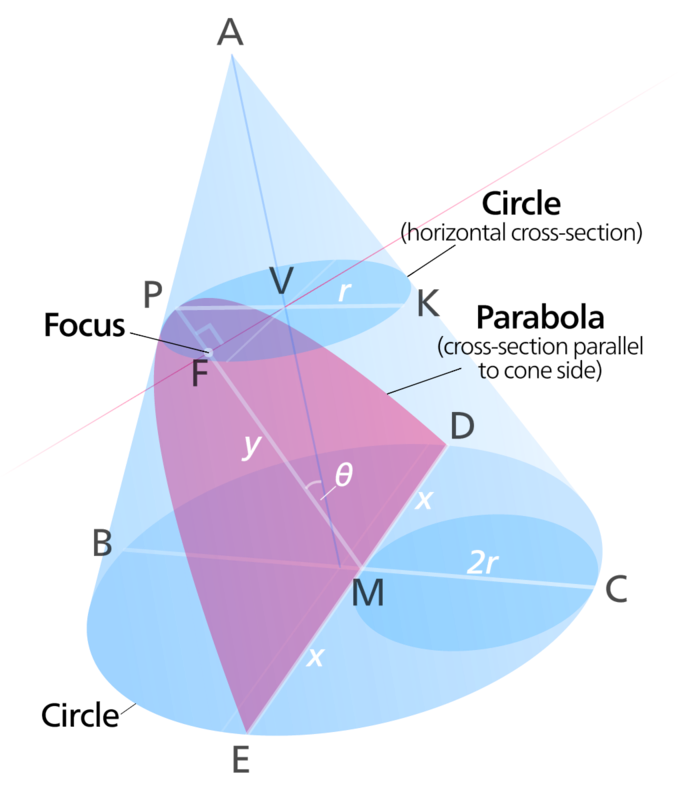
A parabola is a section of a right circular cone formed by cutting the cone by a plane parallel to the slant or the generator of the cone.

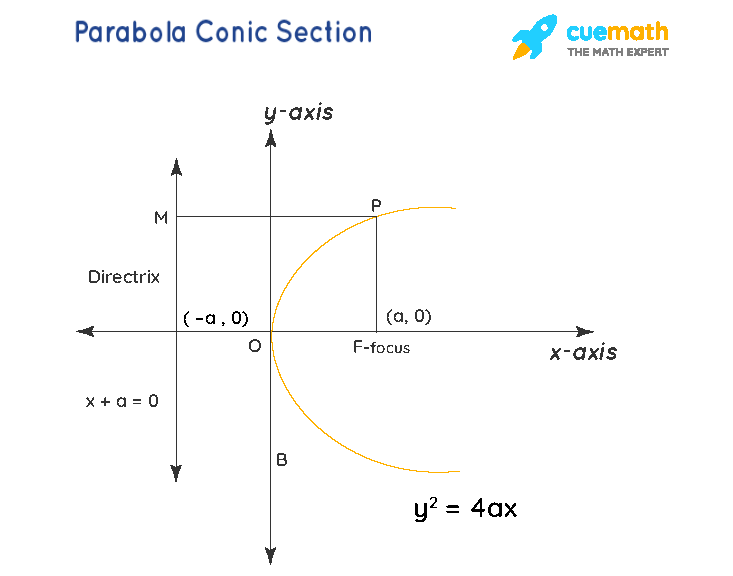
Is conic a parabola. It is the locus of a point which moves in a plane such that its distance from a fixed point is the same as its distance from a fixed line not containing the fixed point. But if you do this, what you get is just part of an elipse, since if the cone and the plane were bigger, eventually you'd end. If the plane is parallel to the generating line, the conic section is a parabola.

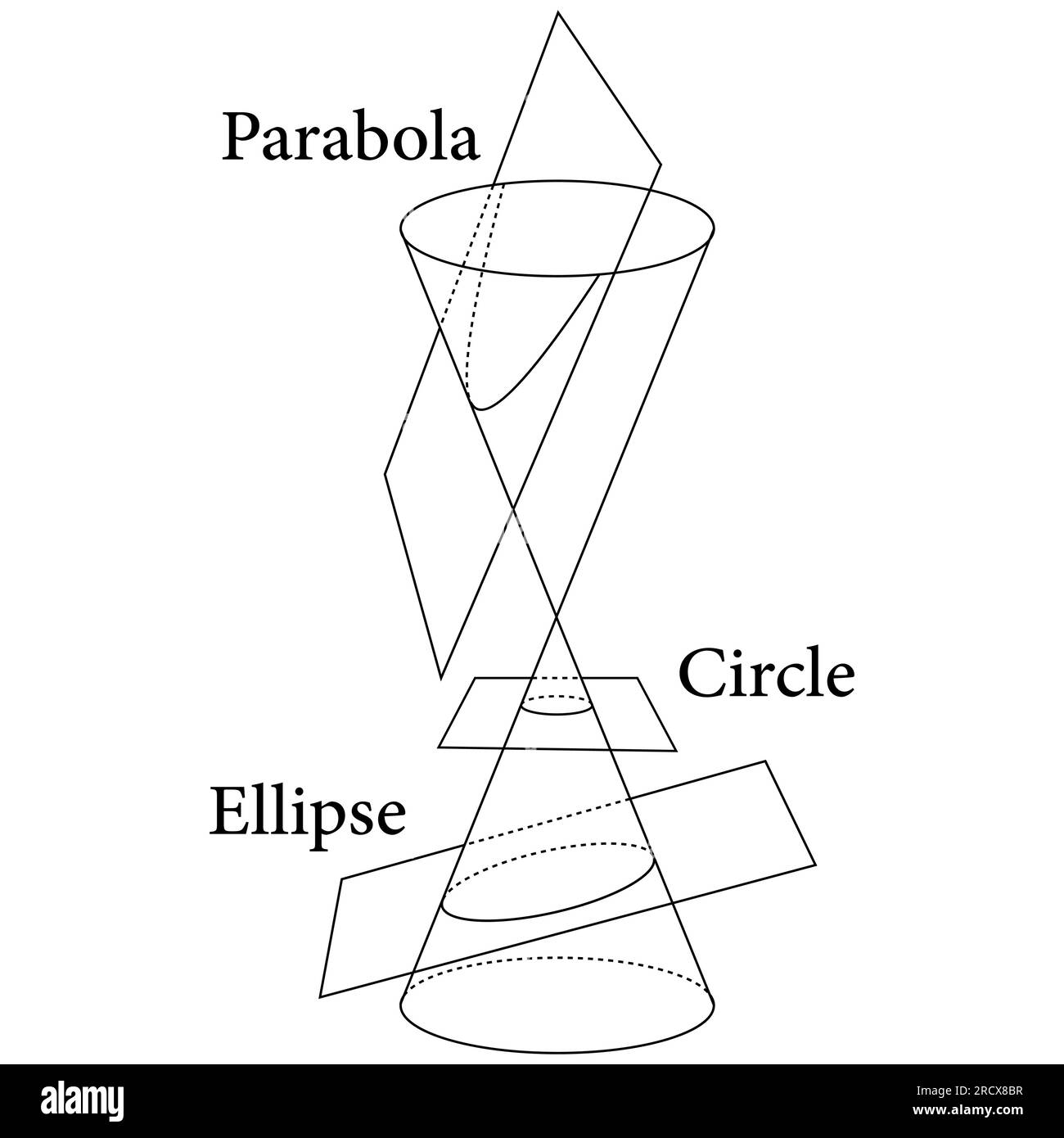
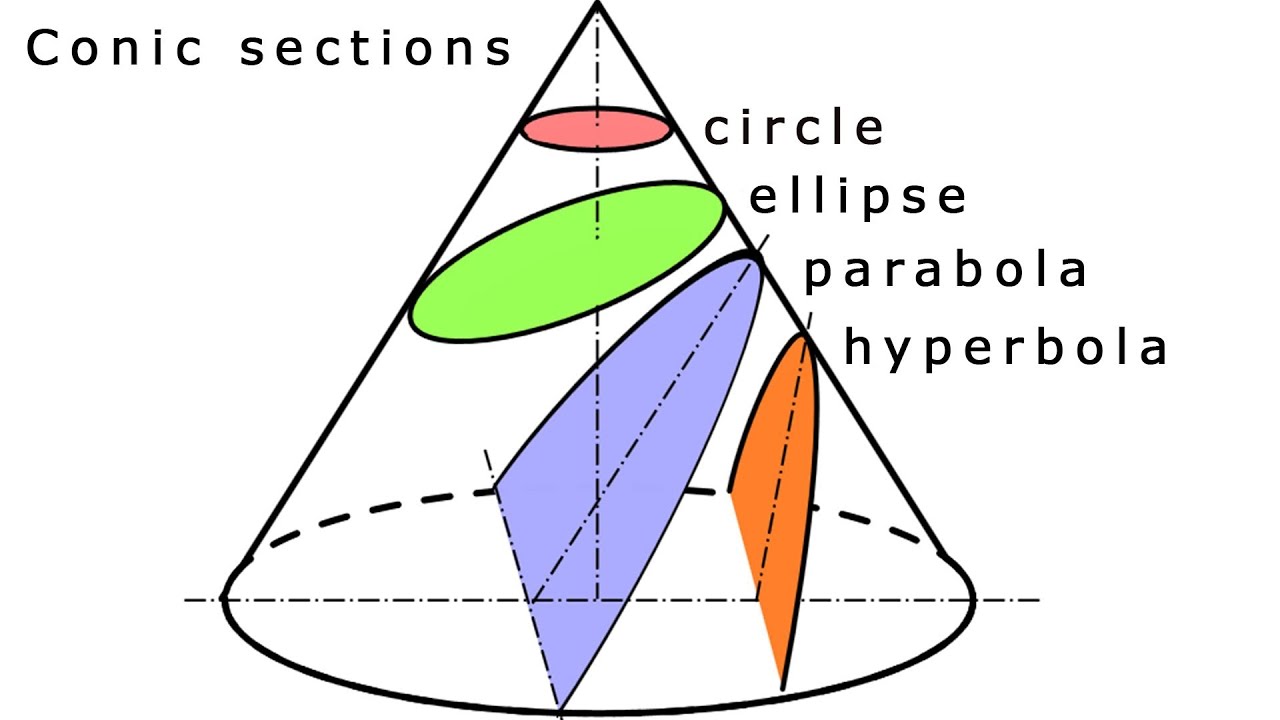
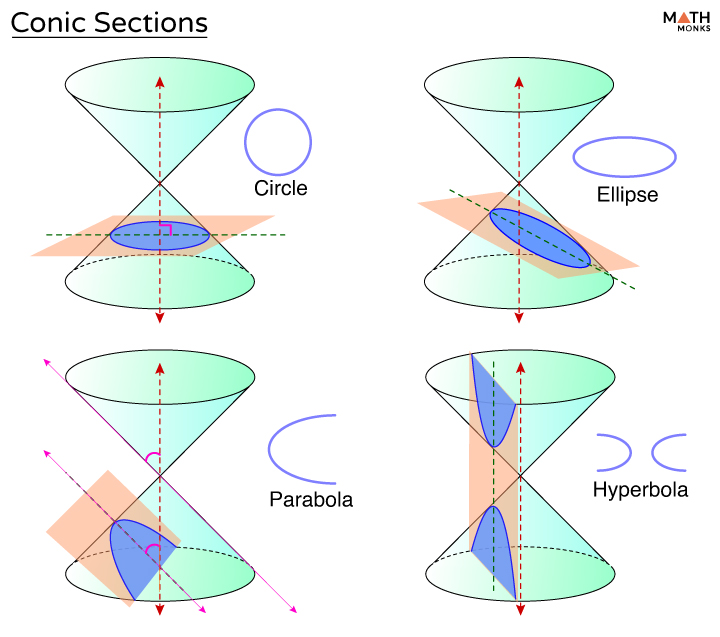
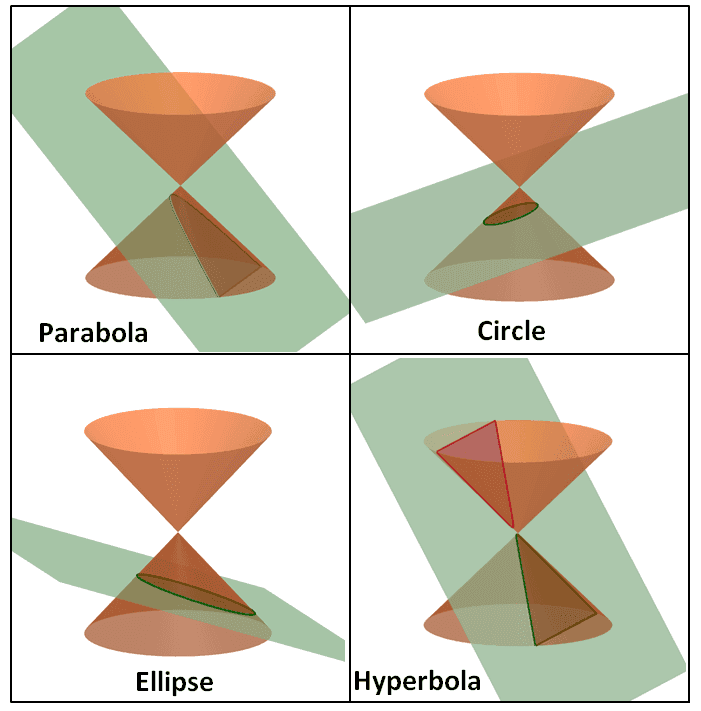
Here is the major axis and minor axis of an ellipse. Conic sections received their name because they can each be represented by a cross section of a plane cutting through a cone. There are four types of conic sections:

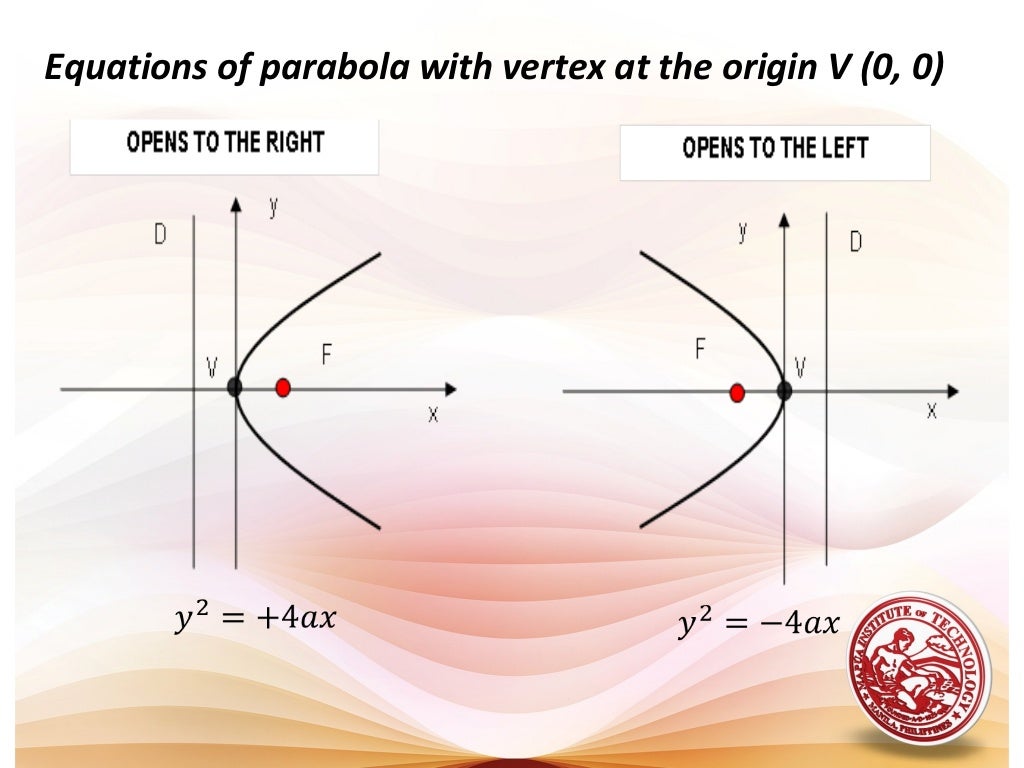
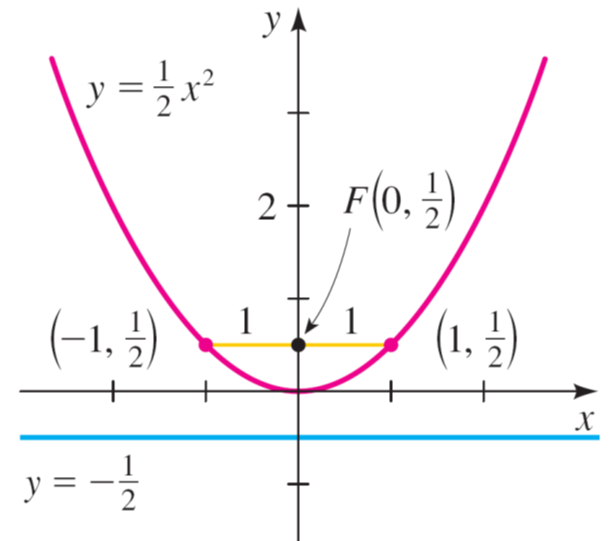
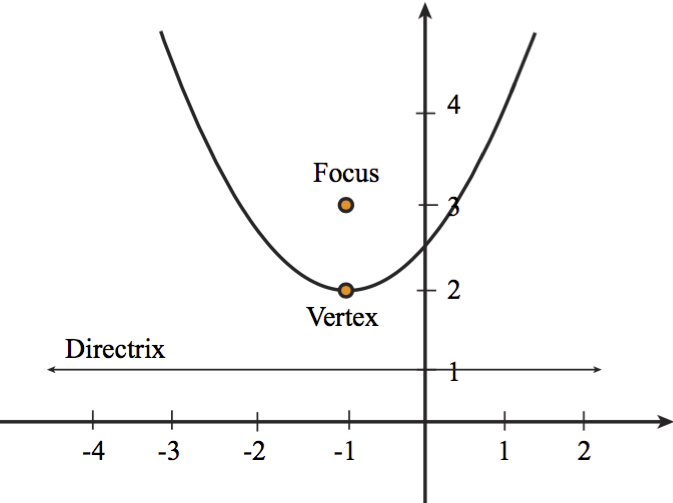
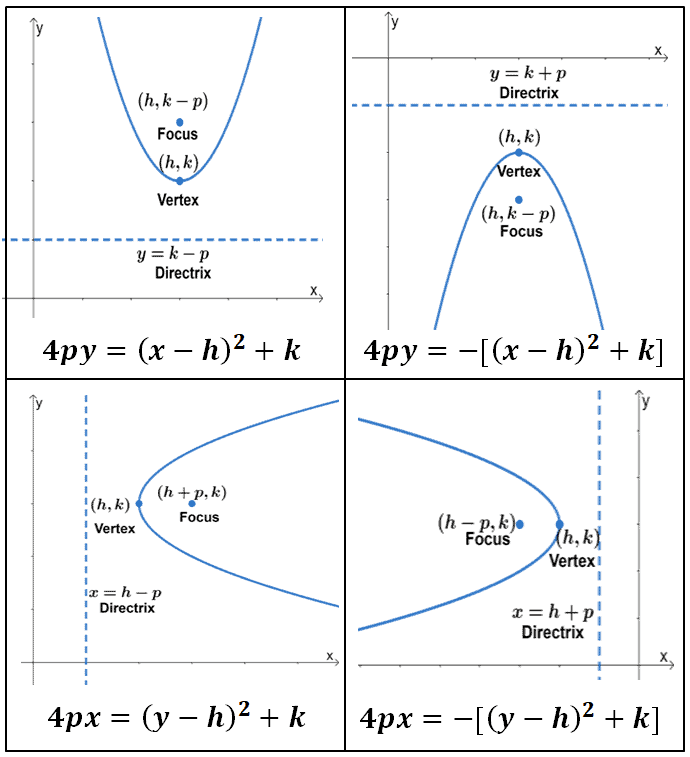
There is a focus and directrix on each side (ie a pair of them). Parabolas as conic sections. In a parabola, is four times the focal length;

Conic sections are the shapes you get when you slice a cone at different angles. These conic are obtained from a simple cone and is obtained by cutting the cone across different sections. If the result is positive and the conic exists, the conic is a hyperbola.

In a circle, is the diameter; We also get a parabola when we slice through a cone (the slice must be parallel to the side of the cone). The three types are parabolas, ellipses, and hyperbolas.

This chapter will examine the circle and the parabola. As these shapes are formed as sections of conics, they have earned the official name conic sections.'' the three most interesting'' conic sections are given in the top row of figure \(\pageindex{1}\). The three types of conic section are the hyperbola, the parabola, and the ellipse;

Conic sections are classified into four groups: We define a parabola as all points in a plane that are the same distance from a fixed point and a fixed line. A conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone with a plane;

A parabola is a particular type of geometrical curve which, algebraically, corresponds to a quadratic equation. Conic sections are generated by the intersection of a plane with a cone (figure \(\pageindex{2}\)). The parabola is a member of the family of conic sections.

Depending on the angle of the plane relative to the cone, the intersection is a circle, an ellipse, a hyperbola, or a parabola. This topic covers the four conic sections and their equations: The next conic section we will look at is a parabola.

The standard form of equation of a conic section is ax^2 + bxy + cy^2 + dx + ey + f = 0, where a, b, c, d, e, f are real numbers and a ≠ 0, b ≠ 0, c ≠ 0. So the parabola is a conic section (a section of a cone). If the plane intersects one nappe at an angle to the axis (other than 90 ° ) ,.