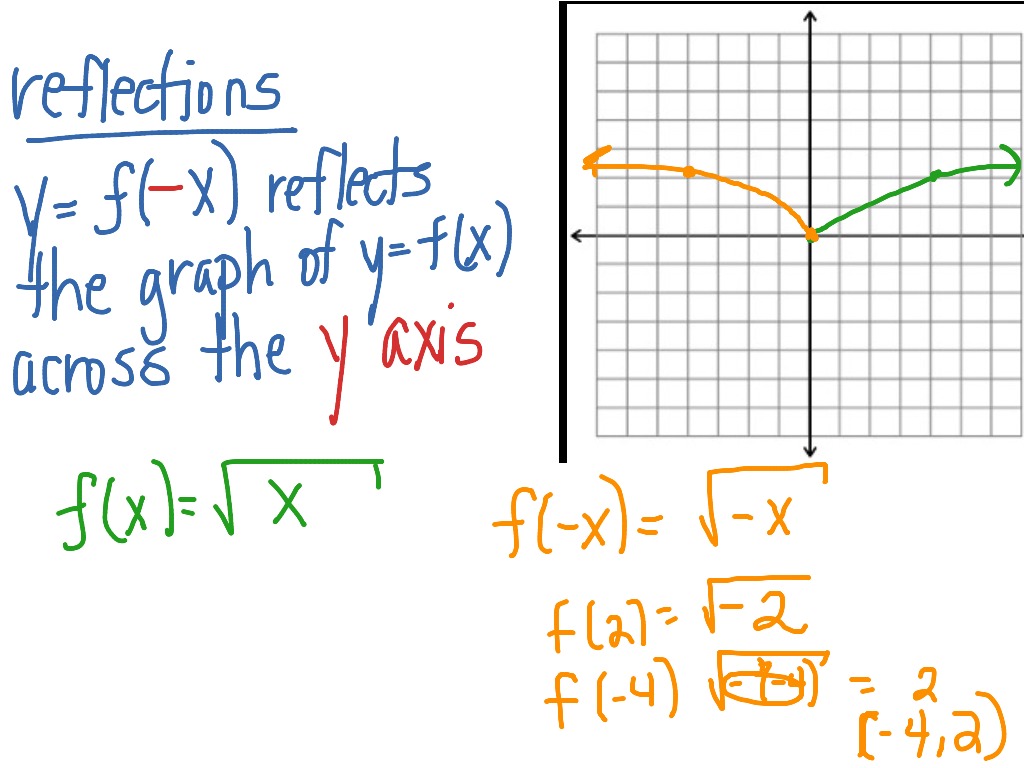Top Notch Tips About Can A Function Cross The Y Axis Twice Add Trendline To Bar Chart
How To Find Intersection Of Two Lines Miller Didettioners Excel Chart With 2 Y Axis Change Horizontal Labels In
Symmetry Of A Graph About Y Axis, X And Origin How To Test For Create Simple Line In Excel S Curve
6.4 Quadratic Functions And Their Graphs Mathematics Libretexts Distribution Graph Excel Geom_line Ggplot2 R
Question Video Identifying The Points Of Intersection A Linear Xy Plot R Reference Line Qlik Sense
Reflection Across The Y Axis Math, Algebra, Functions Showme Ggplot2 Geom_line Legend Excel Change Chart Range
Finding And Understanding Yintercepts (with Examples) Math Bootcamps How To Make A Demand Curve In Excel Matplotlib Simple Line Plot
I want to prove that this function crosses the $x$ axis only twice.
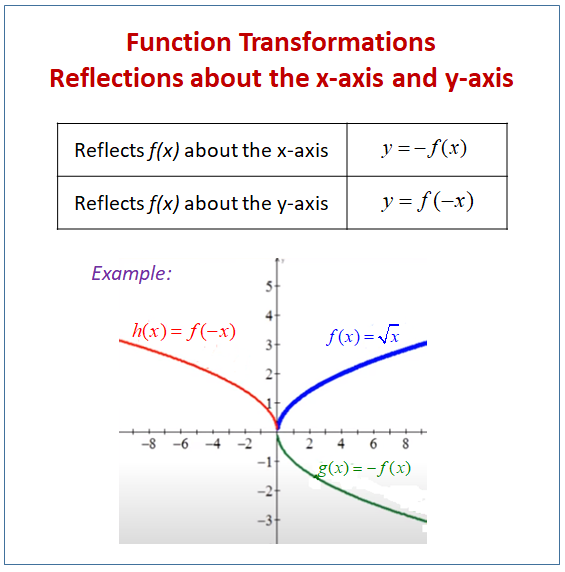
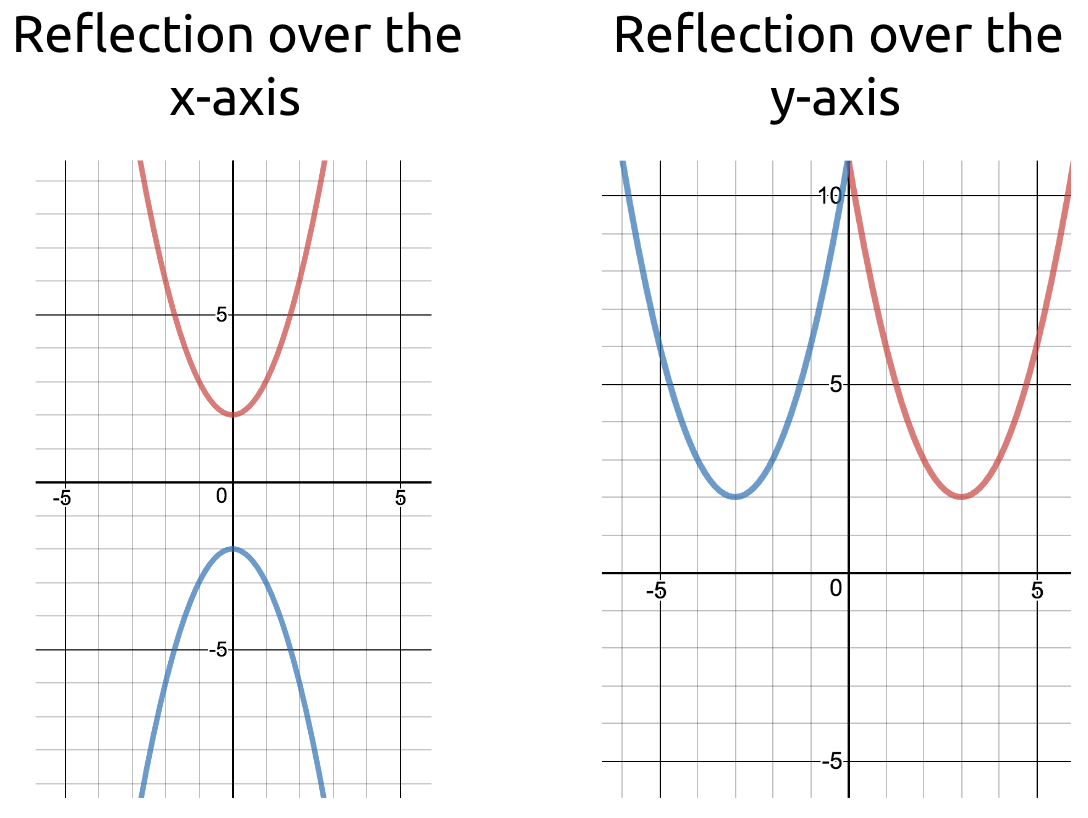
Can a function cross the y axis twice. See the figure below for. A twice differentiable function $f$ satisfies $f′′(x)+f(x)=−xg(x)f′(x)$, $\forall x\ge 0$. If there were, the curve would.
You just need a definition for a crossing point that does not. Want to join the conversation?. This is where two graphs cross, or intersect each other.
For example, look at the graph below: If you write the equation in the form y =. I have this function ($x>0$):
First, we are going to look at intersecting graphs. I'm trying to do this assignment: ( 5 votes) upvote.
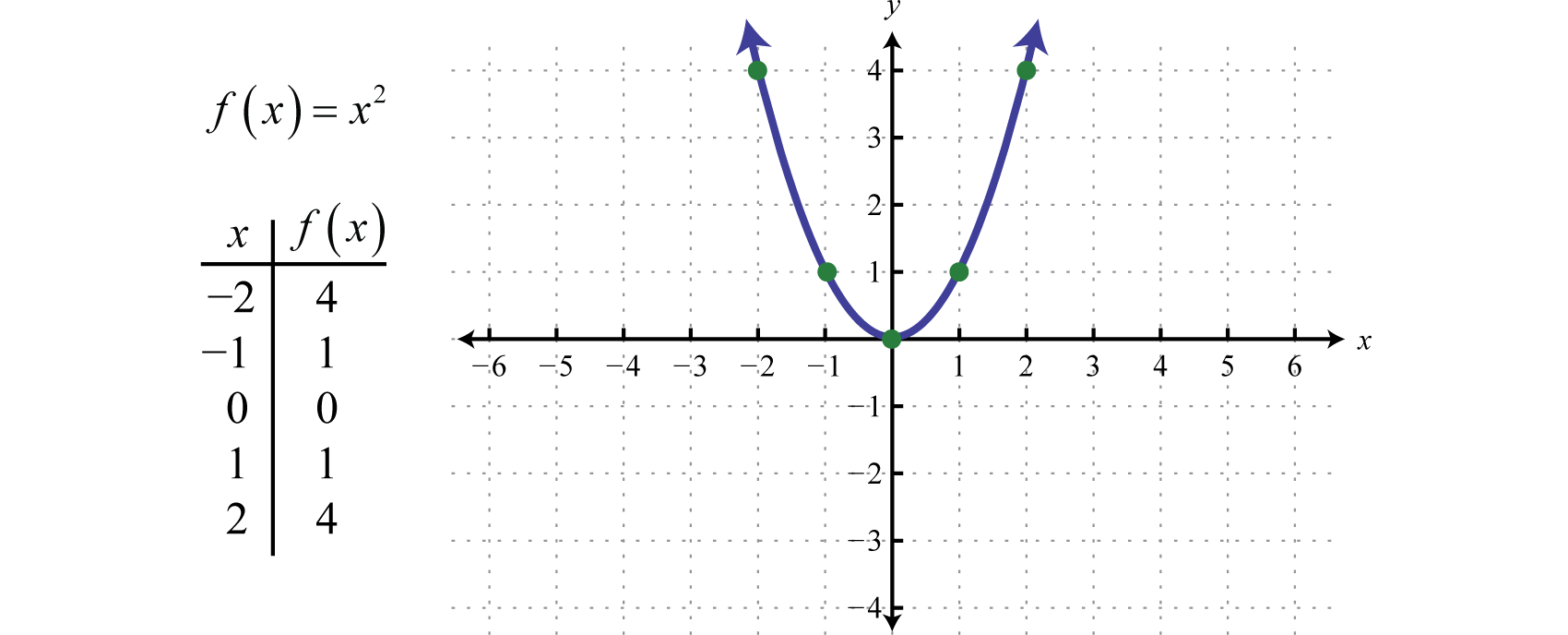
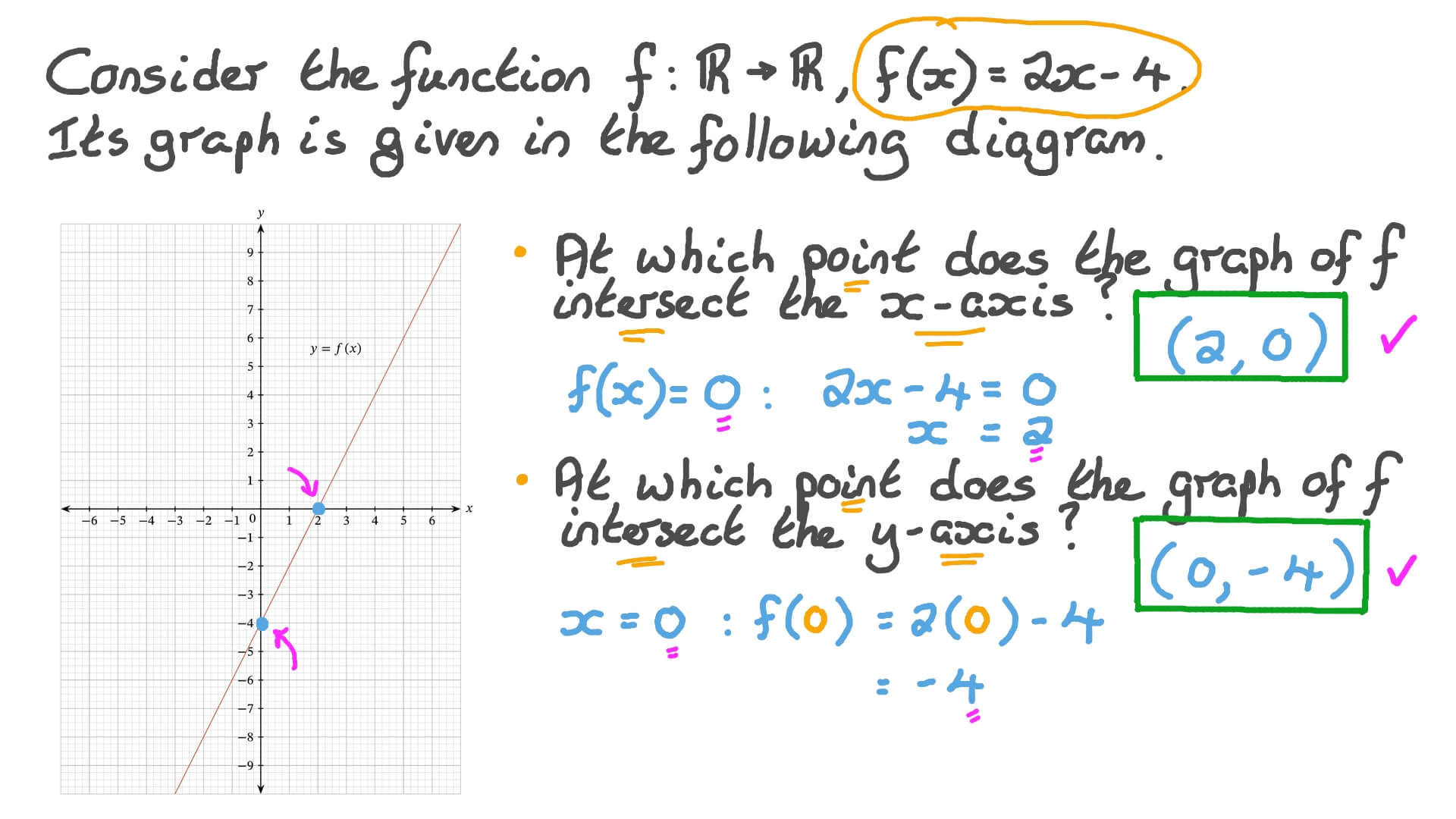
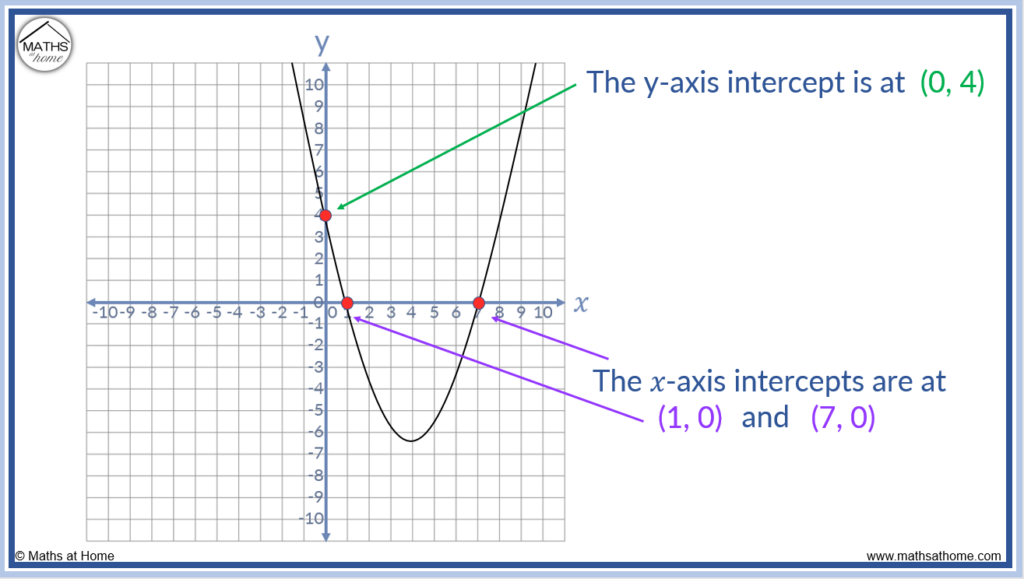
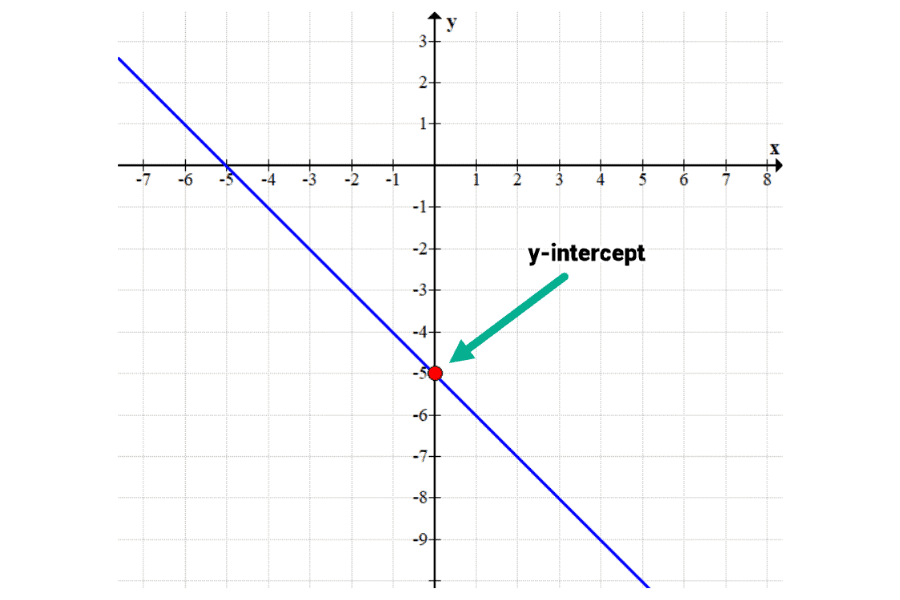
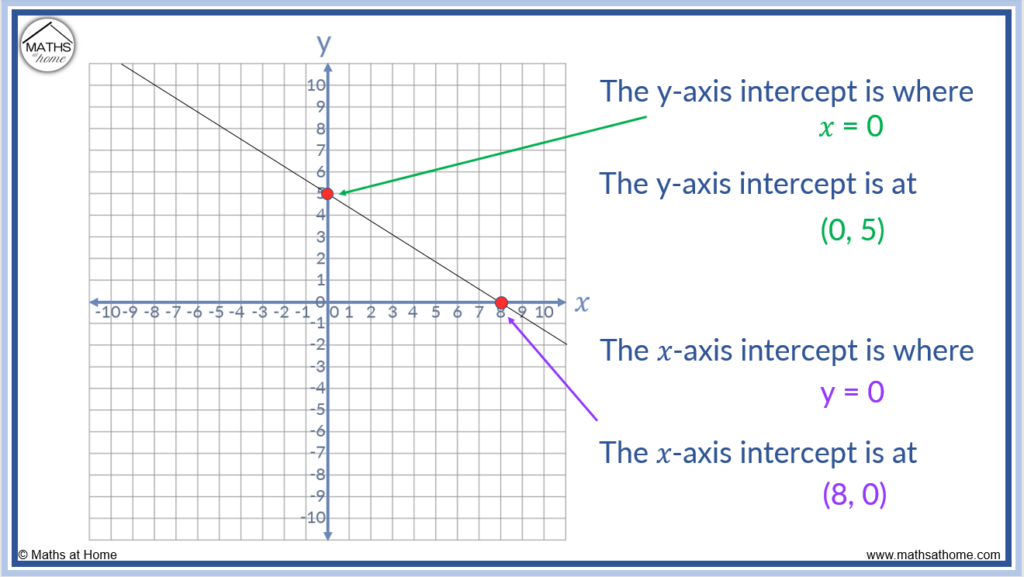
How often, depends on the discriminant. However, the essence of your hypothesis still holds: Looking at the graph, we can find the intercepts.
There cannot be more than one such point, for the graph of a quadratic function.
How To Find X And Y Axis Intercepts Chart Line Js Trend Drawing Software
What Is The Yintercept Explained With Pictures And Examples 034 Scatter Plot Horizontal Line How To A Regression In Excel
[solved] Where Does The Polynomial Y = X^2+ 3x + 4 Cross Yaxis Average Line Excel Plot No Matplotlib
Reflecting Functions Or Graphs (examples, Solutions, Worksheets, Videos Draw Line Ggplot Excel Vertical Graph
Solved 'given The Following Graph, Where Does Line Cross Y How To Draw Axis In Word Chart Js Curved Lines
Equation Of Y Axis With Examples Teachoo Lines Parallel X Or A Stacked Area Graph How To Make Line In Excel 2010
How To Find X And Y Axis Intercepts Do You Change The Values In Excel Add Line Ggplot2
How To Find X And Y Axis Intercepts Do You Make A Line Graph On Google Sheets Segment
2.3.1 Example 1 Finding The Maximum/minimum And Axis Of Symmetry A Less Than On Number Line Git Command Graph
[solved] F(x)=x^3 Reflected Over The Yaxis And Horizontally Compressed X Axis Y In A Bar Graph 3 Line Break Indicator
Transformation Of Graphs Reflection In Y Axis Numberolfe How To Make Line Graph On Google Sheets Ignition Time Series Chart
Reflect Function About Yaxis F(x) Expii Plot Lm In Ggplot2 Regression Line Graph Maker
How To Find X And Y Axis Intercepts Do A Line Graph On Google Sheets Tableau Confidence Interval Chart
Question Video Finding The Coordinates Of Intersection Point How To Make A Derivative Graph In Excel Pivot Chart Multiple Lines
X And Y Axis Gcse Maths Steps, Examples & Worksheet Plotting Dates In R How To Put A Trendline Excel
The Graph Of Linear Equation 2x + 3y = 6 Cuts Y Axis At Lucidchart New Line Excel Three
Graph Transformations Gcse Maths Steps & Examples How To Change The Bounds Of A Chart In Excel Easy Line Maker
4. Based From The Graph On Right, At What Point Does Geom_line Multiple Lines Charts_flutter Line Chart
