Supreme Tips About How Is A Smooth Curve Different From Regular Ggplot Multiple Lines By Group

A curve is a continuous and smooth flowing line without any sharp turns and that bends.

How is a smooth curve different from a regular curve. In applications, when you say the curve is smooth it means till the derivatives you are interested in the curve has to be continuous. Equivalently, we say that α is an immersion of i into r3. Complex) solution than (0, 0, 0).

For an algebraic curve of degree n, with , the curve is smooth in the real (resp. A smooth curve α: So for instance in green's theorem,.

Differentiating with respect to y y, one can see that the curve is smooth wherever z ≠ 0 z ≠ 0, and substituting in z = 0 z = 0, one can see the curve is smooth. (a) a smooth curve in rn is a smooth (that is, in nitely di erentiable) map : In the general context, regular is a property of a scheme (or a ring, or local ring), and smooth is a property of a morphism of schemes.

Equivalently, we say that is an immersion of i into r3. In this article, these curves are sometimes called topological. The curve (t) = (t3, t2) in the plane fails to be regular when t = 0.

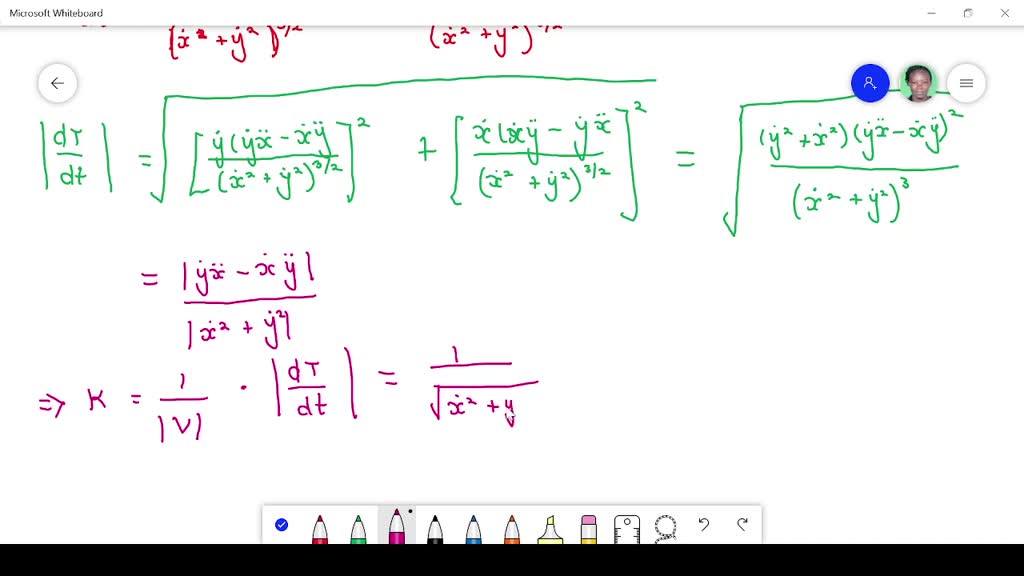
Learn about curved shapes, types of curves, examples, facts, and more. The curvature is the length of the vector $$ \frac{\gamma'\times\gamma''}{\left|\gamma'\right|^3}\tag{2} $$ which is smooth because. A curve $\mathbf{r}(t)$ is considered to be smooth if its derivative, $\mathbf{r}'(t)$, is continuous and nonzero for all values of $t$.

Kernel regression scales badly, lowess is a bit faster, but both produce smooth curves. I → r3 is said to be regular if α'(t) ≠ 0 for all t ∊ i. A smooth curve is a curve which is a smooth function, where the word curve is interpreted in the analytic geometry context.

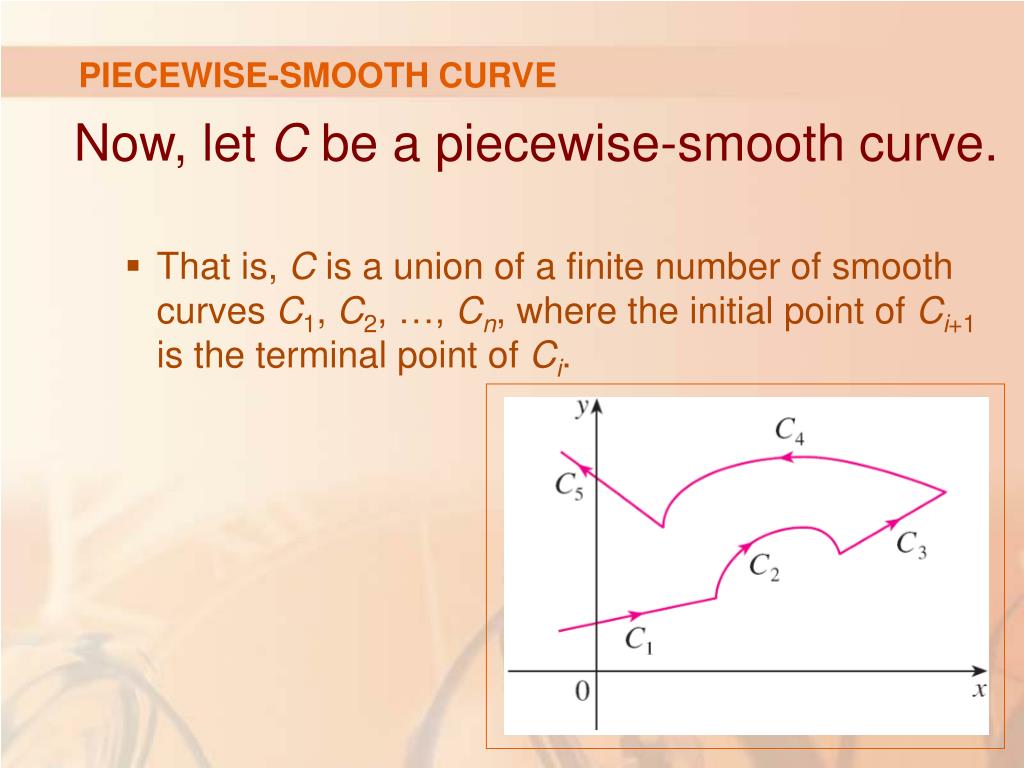
In this video, i show that a curve described by a vector function is not smooth by showing there are values of t that make the derivative equal to zero. A piecewise smooth curve is a curve c that can be broken into finitely many smooth pieces c 1 c 2,., c n where the terminal point of one piece is the initial point of the next. The torsion indicates how much the normal changes, in.

We define the positive direction on a contour \(c\) to be the direction on the curve corresponding to. The curvature indicates how much the normal changes, in the direction tangent to the curve. Complex) projective plane if the system has no other real (resp.

The curve α(t) = (t3, t2) in the plane fails to be. Where iis an open interval of r (so icould be (a;b) or (1 ;b) or (a;+1) or r). The curve is a smooth curve if the derivatives f′ f ′, g′ g ′, h′ h ′ exist and are continuous in [a, b] [ a, b] the curve is a regular curve or a regular smooth curve, if it's smooth and also the three derivatives f′ f ′, g′ g ′, h′ h ′ are not simultaneously zero for.

A smooth curve : X(t) = t3, y(t) = t6. In particular, a smooth curve is a.