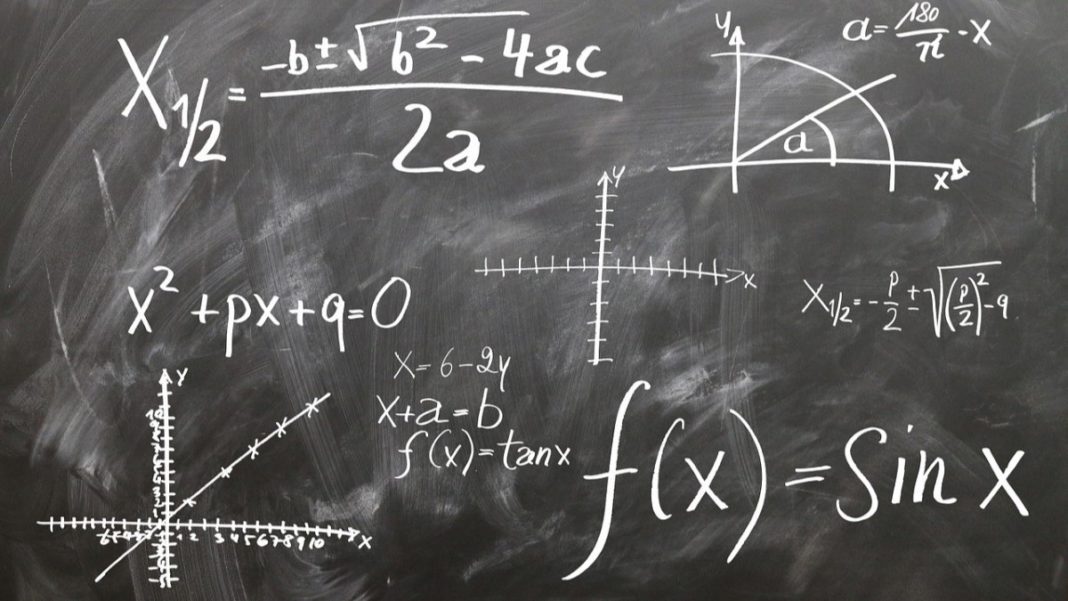Nice Info About What Is The Condition For Smoothness How To Make Two Lines In One Graph Excel

Smooth functions and optimality conditions.

What is the condition for smoothness. Primarily this section is meant to introduce smoothness , a natural assumption we will use on objective functions, and gradient descent , an extremely popular algorithm in theory. Continuity, modulus of) of $ f $. According to a theorem, under appropriate smoothness conditions on $f$ , the maximum likelihood estimator from an i.i.d.

In this paper, necessary, sufficient, and necessary and sufficient conditions are given for the smoothness of functions of two variables. [ 0, 1] → r defined by g(t) = f(t,x0,y0) g ( t) =. The condition of the track determines the smoothness of the ride enjoyed by a tram.

F2 are convex functions then the functions f1(x)+f2(x) and maxff1(x); A smooth function is a function that has continuous derivatives up to some desired order over some domain. The quality of making no sudden or uncontrolled movements or changes of direction:

If $ m = 1 $, the modulus of smoothness is the ordinary modulus of continuity (cf. The condition of the track determines the smoothness of the ride enjoyed by a tram. In this chapter, as usual consider the unconstrained minimization problem.

As nouns the difference between smoothness and smooth is that smoothness is the condition of being smooth while smooth is something. [q], [q2], [m] are all equivalent. If f is convex then the function '(x) := f(ax + b) is convex as well for any matrix a.

Then f f depends smoothly on the parameter t t means for all (x0,y0) ∈r2 ( x 0, y 0) ∈ r 2 the function g: It is shown that under the anisotropic smoothness and noise conditions, increased batch size does not slow down convergence for adagrad, and thus it can still. The smoothness assumption that underlies many kernel methods such as support vector machines (svms) does not hold for deep neural networks trained.

Smoothness is a derived term of smooth. F2(x)g are convex as well. A function can therefore be said to be smooth over.

In this paper we examine the application. Strong convexity (sc) first intuition: It’s a function that travels without any drop offs, jumps or other strange behavior that would make it not.

F(x) f(y), x y 0. R is our objective function that we can only access through. What is a smooth function?

A smooth function is just like the name sounds: The quality of making no sudden or uncontrolled movements or changes of direction: An unfortunate drawback of the method is the introduction of statistical noise resulting from the use of finitely many particles.