Recommendation Info About How Do You Describe A Curve Graph Add Vertical Line Excel

When asked to describe patterns in graphs, you ‘say what you see’.

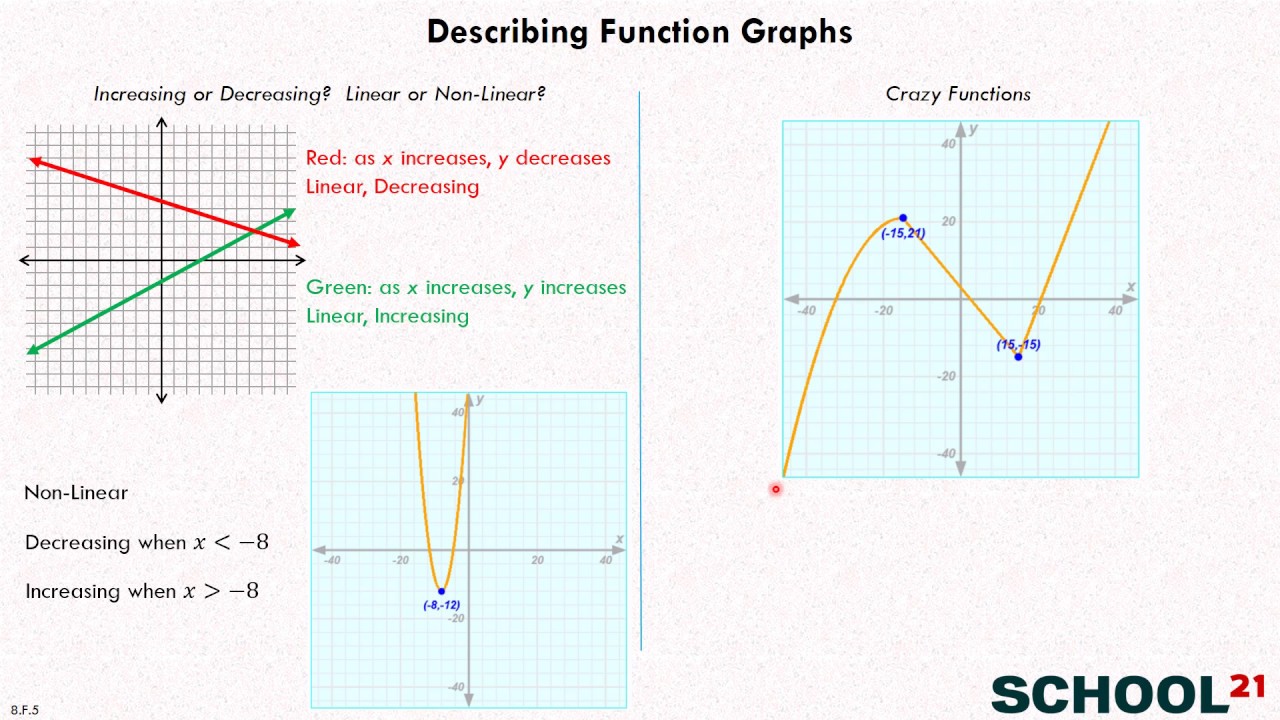
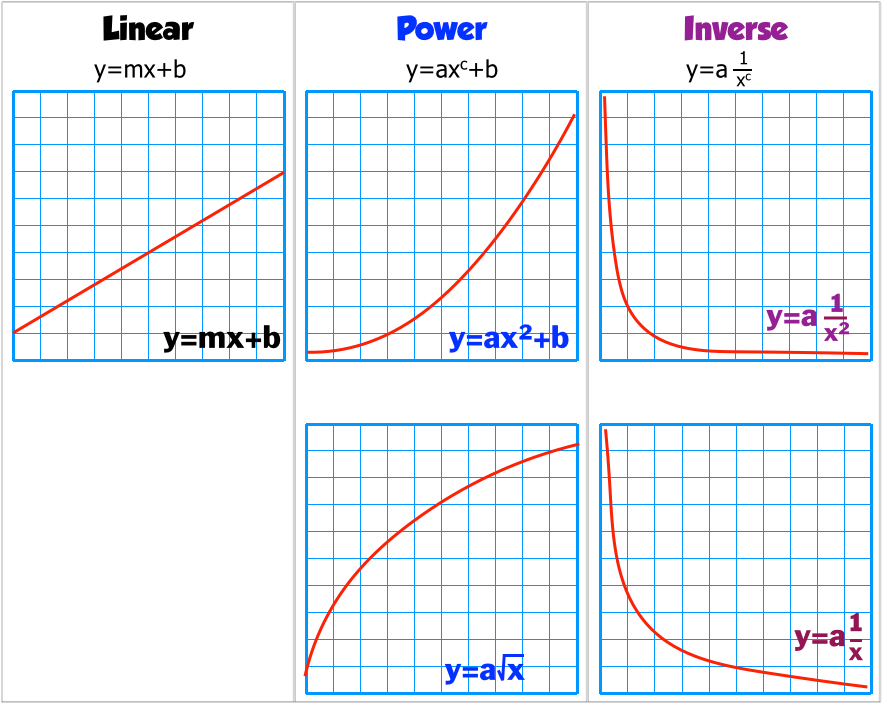
How do you describe a curve graph. Identify key features. There are four possibilities for graph shapes that we will deal with. Is the association linear or nonlinear?

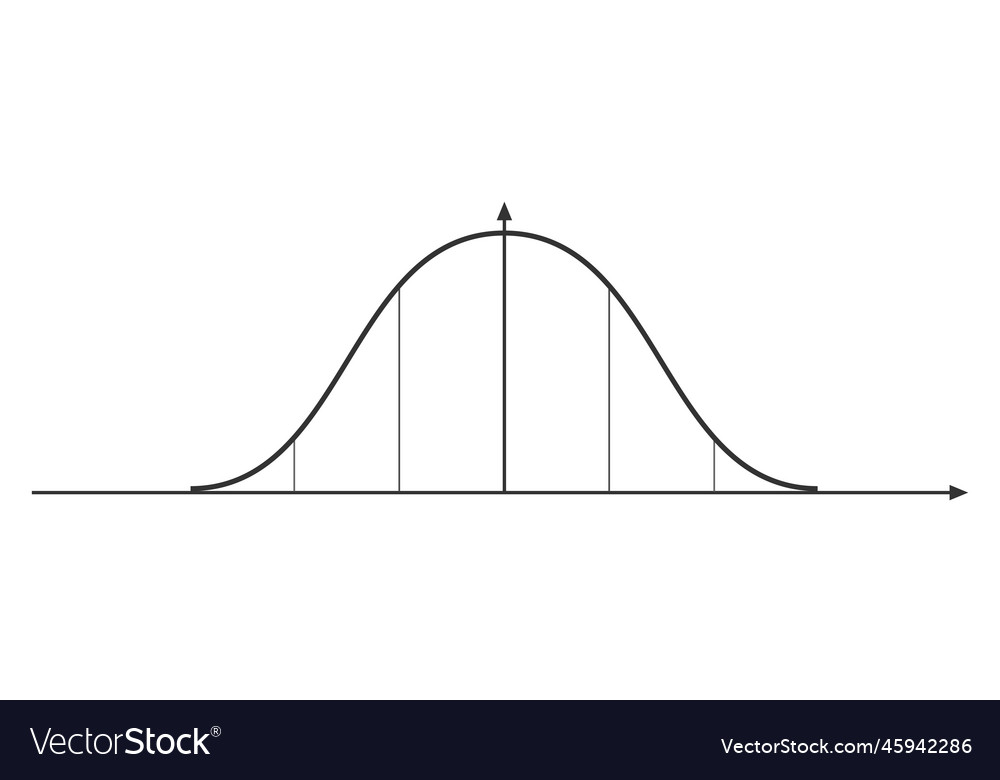
This is a formal definition of the word curve. When a curve lies in a plane (such as the cartesian plane), it is often referred to as a plane curve. It represents a graph where the data clusters around the mean, with the highest frequency in the center, and decreases gradually towards the tails.

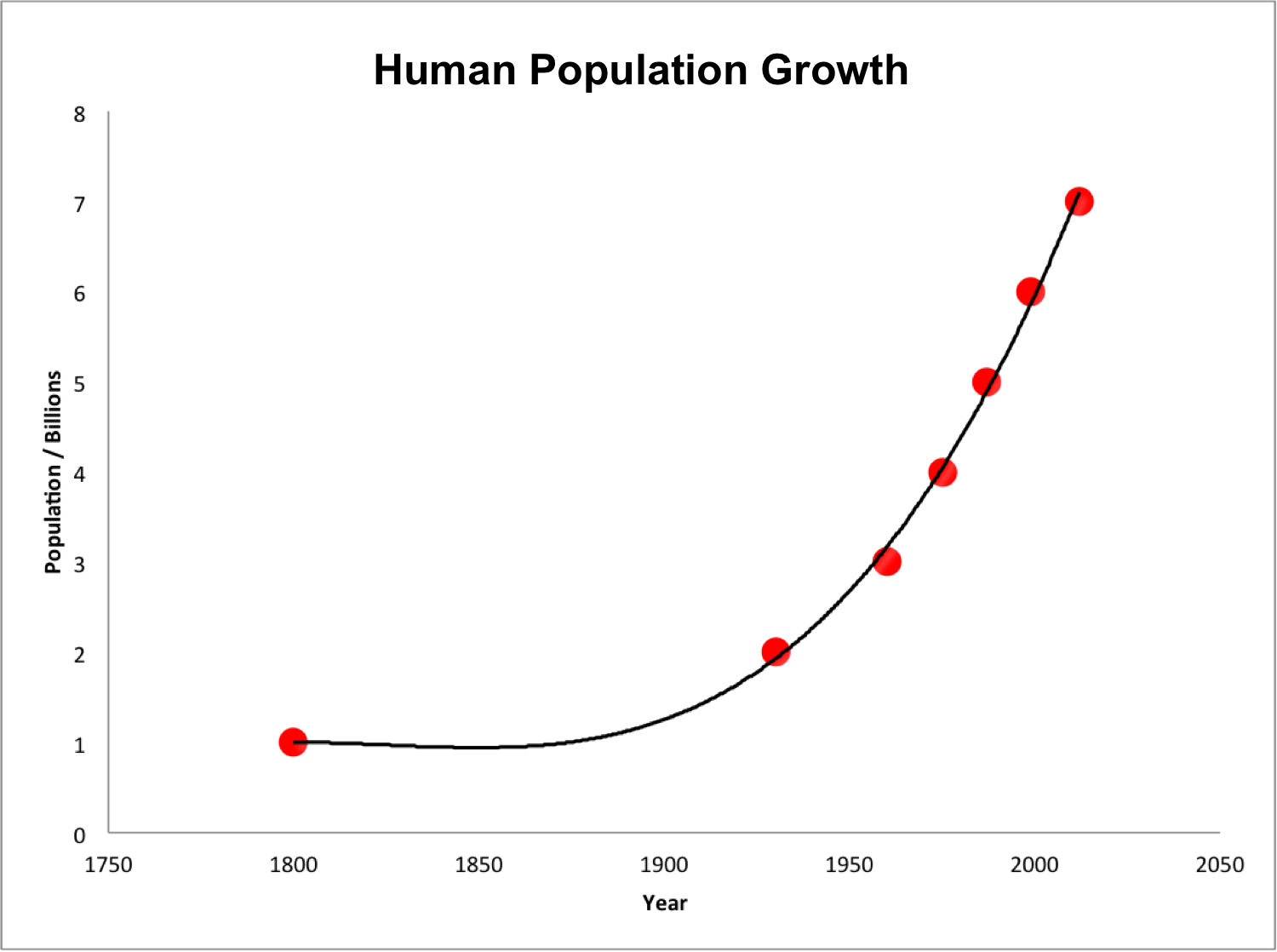
Peaks represent rapid growth periods, whereas valleys highlight declines. Describing the graph’s shape provides immediate visual insight into trends and patterns.

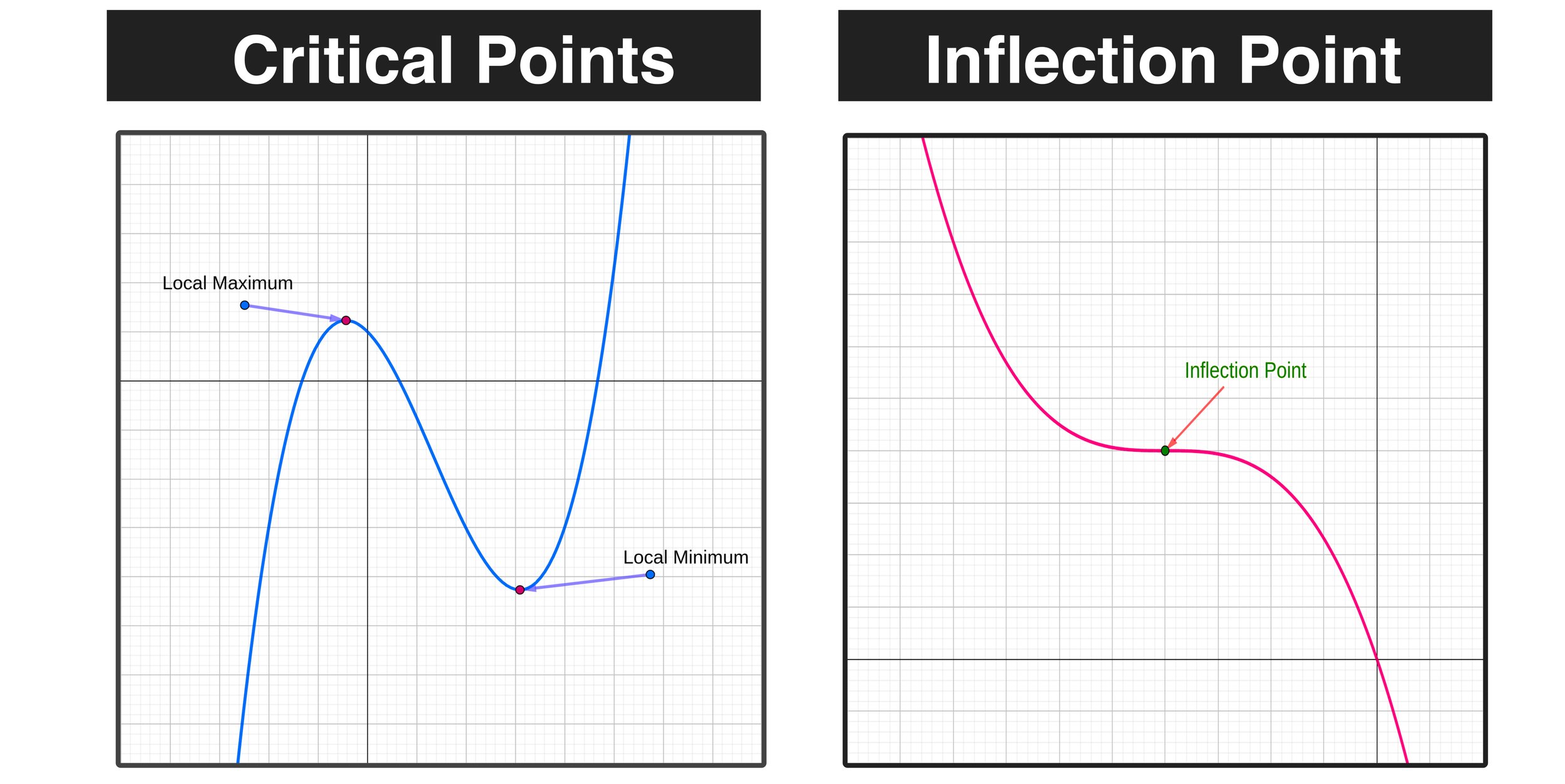
Define the slope of a curve. Looking for an introduction to parabolas? How to ‘describe’ graphs.

In figure \(\pageindex{2c}\) we show a graph of \(f\) drawn with a computer program, verifying the accuracy of our sketch. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. It then provides practice in describing a range of different lines (peak, plummet, etc.).

In ielts, it should be pretty obvious what you are given because the only three graph types you have are: From there, you can describe the key variables that make up the graph. A curve is a graph along with the parametric equations that define it.

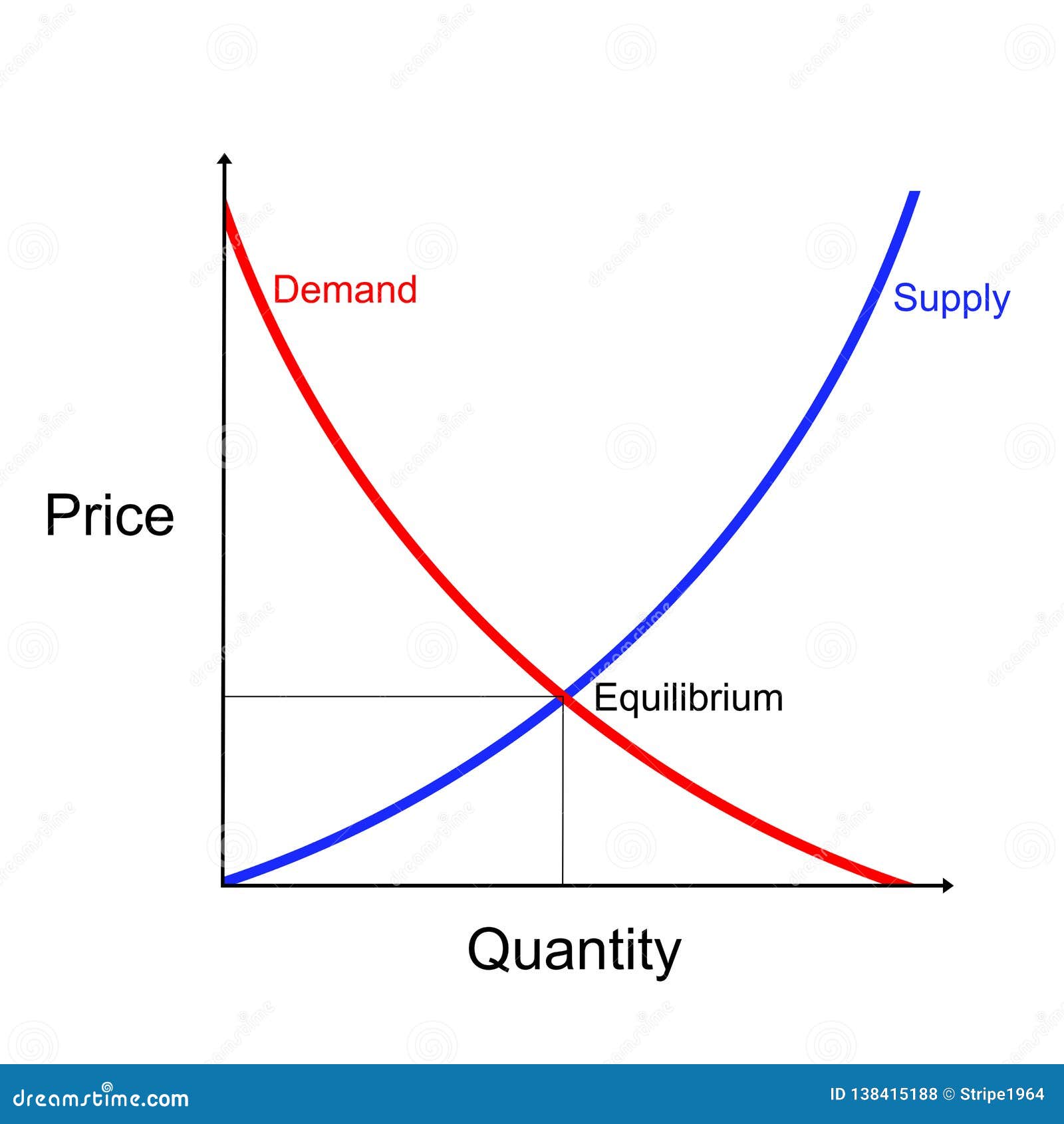
A curve is a shape or a line which is smoothly drawn in a plane having a bent or turns in it. Such charts show relationships between two variables and help to identify correlations or patterns. Plane or two dimensional geometry.

Geometry can be classified into two types. Here are some examples from the real world. How do they differ from each other?

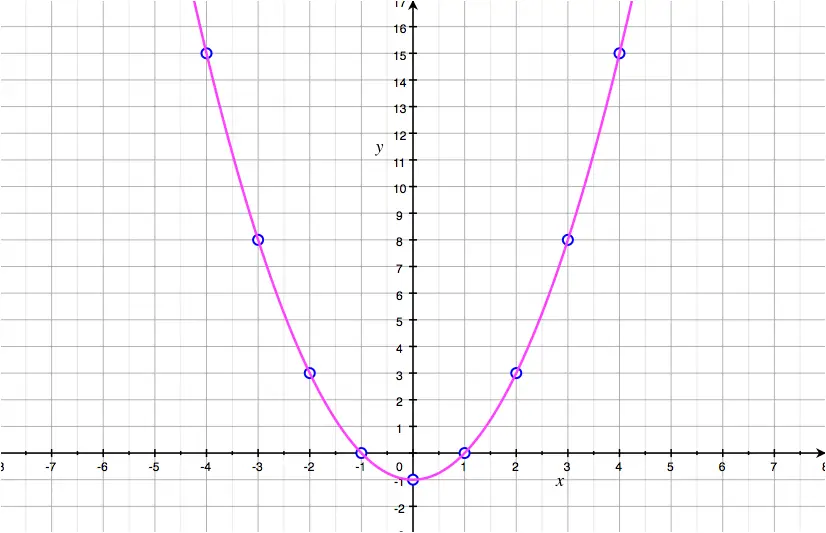
It turns out, quite a lot! Let's see if we can use everything we know about differentiation and concativity, and maximum and minimum points, and inflection points, to actually graph a function without using a graphing calculator. This equation is in vertex form.

Analyze polynomials in order to sketch their graph. What can calculus tell us about curve sketching? For example, you can make a curve of the unitcircle by the equation $x^2+y^2=1$ a function is a subset of the family of curves with the restriction that for each $x$ there is exactly one $y$ (or ($f.