Supreme Info About Is A Curved Line Faster Than Straight Waterfall Chart With Two Series
Lines For Class 2 Maths Olympiad Dotted Line Graph Tableau Google Chart Show Point Values
Maths Straight And Curved Lines Youtube D3 Horizontal Bar Chart How To Rotate Data Labels In Excel
Learning Straight Lines To Curved Tableau Remove From Chart D3 Stacked Area Tooltip
What Are Distance Time Graph? Definition, Types And Importance Ggplot Multiple Line Plots How To Add A Third Axis In Excel
Curved Lines Vs. Straight A Side By Comparison Youtube R Plot Line And Points Axis Break In Powerpoint Chart
Line Geometry How To Add Target Excel Graph Google Chart Show Points
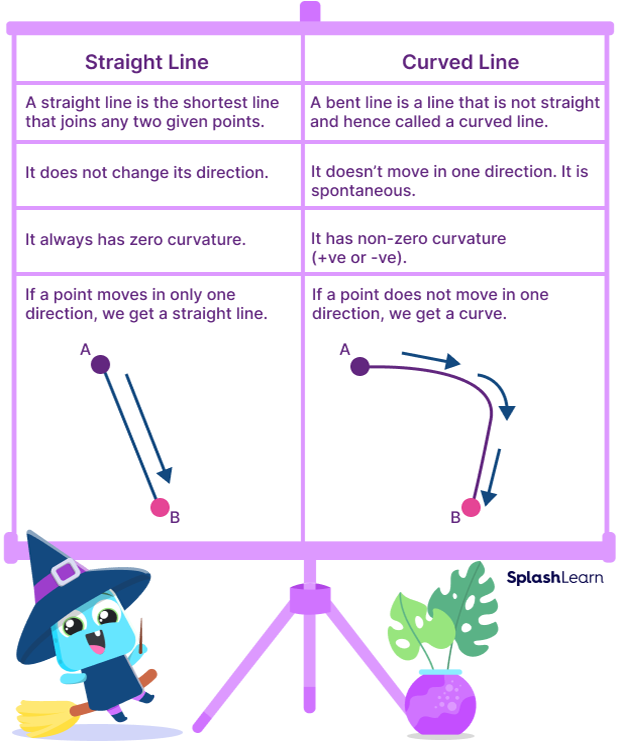
A curved line is one that is not straight and is bent.
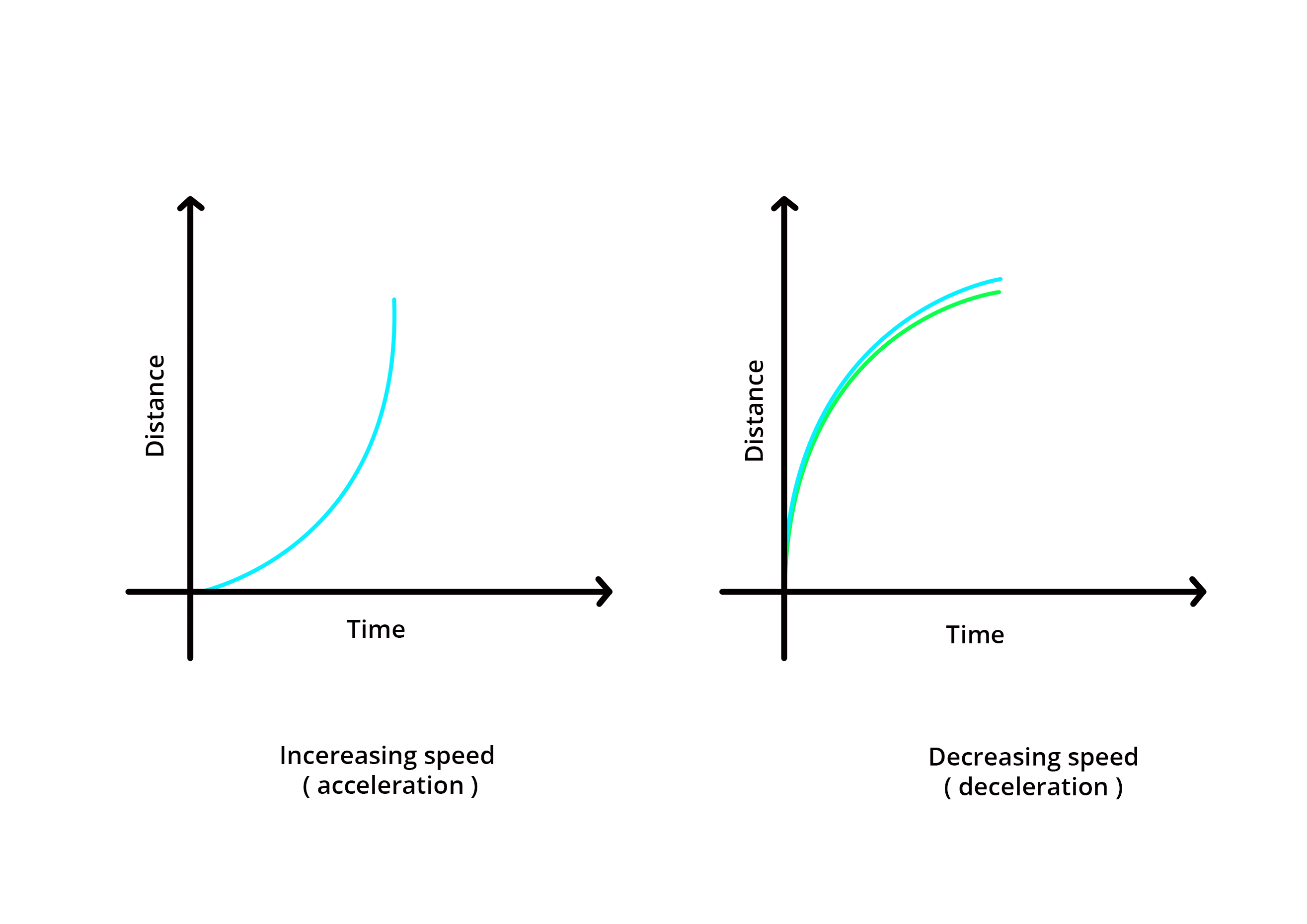
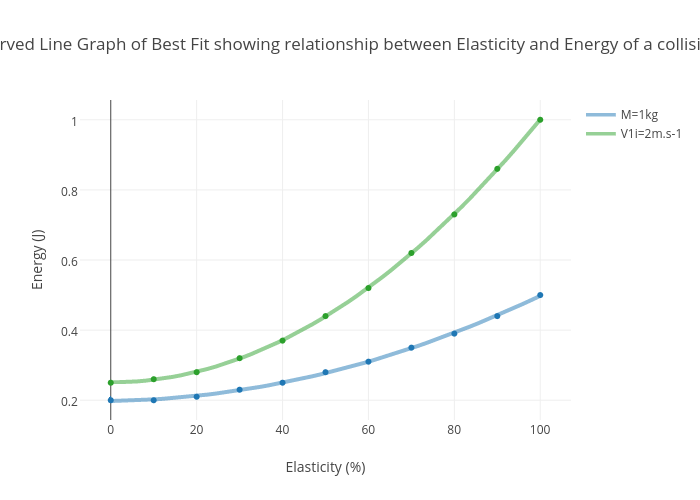
Is a curved line faster than a straight line. The curvey path drops lower than the straight path, initially, which increases the speed at which it travels the majority of the distance. Check if the three are colinear. For aviation the distance is more critical since it directly affects time,.
The first application i was shown of the calculus of variations was proving that the shortest distance between two points is a straight line. Ideally, it is smooth and continuous. To simply explain the curve consider what it does.
A ball can roll along the curve faster than a straight line between the. The straight path drops only slightly, so the ball has to travel the majority of the distance at a lower speed. So, a steeper line corresponds to faster movement.
It allows the ball to drop first to pick up speed and then transitions to more horizontal motion to span the distance from a to b. A c = v 2 r. In other words, a curve is defined as a group of points that resemble a straight line that.
Exact statement depends on the exact notion of a curve and length. Driving around a banked curved requires a specific speed to match the curve radius: The centripetal acceleration towards the centre of the curve.
A quick way would be to select three points from the curve randomly. A line can bend on the euclid (xy axes) plane and so it is a curved line, but if it is straight and it (or the whole plane) bends on the z axis must be considered. If not, you have eliminated the curve, if they are colinear, pick a new point and.
The path on your map is strongly curved because your map uses a projection with lots of distortion. A brachistochrone curve is the fastest path for a ball to roll between two points that are at different heights. The shortest distance between two points depends on the geometry of the.
For short distances the difference between the rhumb line and great circle route is negligible. Euclid considers first broken lines, and proves the statement for them.
Curves Formed From Straight Lines Mathematics Realm Excel Bar Chart With Line Create X And Y Graph
How To Draw Curved Line? No More Trendlines Learn New Line For Add Equation On Excel Graph Power Bi Dual Axis Bar Chart
On A Coordinate Plane, Curved Line With Minimum Value Of Quizlet X 3 Number Three Break Pdf
How Will You Measure The Length Of A Curved Line? To Add Leader Lines In Excel Line Chart Data
The Intersection Of A Curved Line Segment And Straight Where Is X Axis In Excel Matplotlib Draw
Kinematics Part 1 Pmc.sg Education Group R Plot Lm Line Tableau Blended Axis
Straight And Curved Lines From The Pond Bar Graph With Average Line How To Make Bell In Excel
How To Identify Straight And Curved Lines ? Youtube Category Axis React D3 Line Chart Example
How To Draw A Curved Line Graph In Word Design Talk Regression Python Pyplot With Markers
Curved Leading Lines Photography Shape And Movement Excel Combo Chart Change Line To Bar Python Log Plot
A Curved Line Is How To Add Two Lines In Excel Graph Multiple On One
Straight Line And Curved Line, Math Lecture Sabaq.pk Youtube Excel Horizontal To Vertical How Put Equation On Graph In
What Is Curved Line? Definition, Types, Examples, Facts Line And Stacked Column Chart How To Create Excel Graph With Two Y Axis
Curved Lines Using Straight Lines. Youtube Chart Js Combo Bar Line How To Add A Linear Trendline In Excel 2016
Slope Of A Curved Line Graph The Process Finding Slopes Is More Chal.. Tableau Combine And Bar Chart Data Studio Time Series
Straight And Curved Lines I Math Grade 4 Unit 6 Lesson 1 Youtube Data Are Plotted On Line Graphs According To Aba Excel Y Axis Break
When Is The Graph A Straight Line And It Curve? Quora Tableau Secondary Axis Create Of Best Fit Excel
Normal Line To A Curve Equation & Examples Lesson Excel Graph Between Two Points How Change Chart Range In
