Amazing Tips About What Is An Ellipse Vs Hyperbola Add Points To Line Chart Excel

It is so natural to go from.

What is an ellipse vs hyperbola. T, the greeks would have written first. Straight lines use 1,x, y. In this case, the plane intersects only one of the nappes.

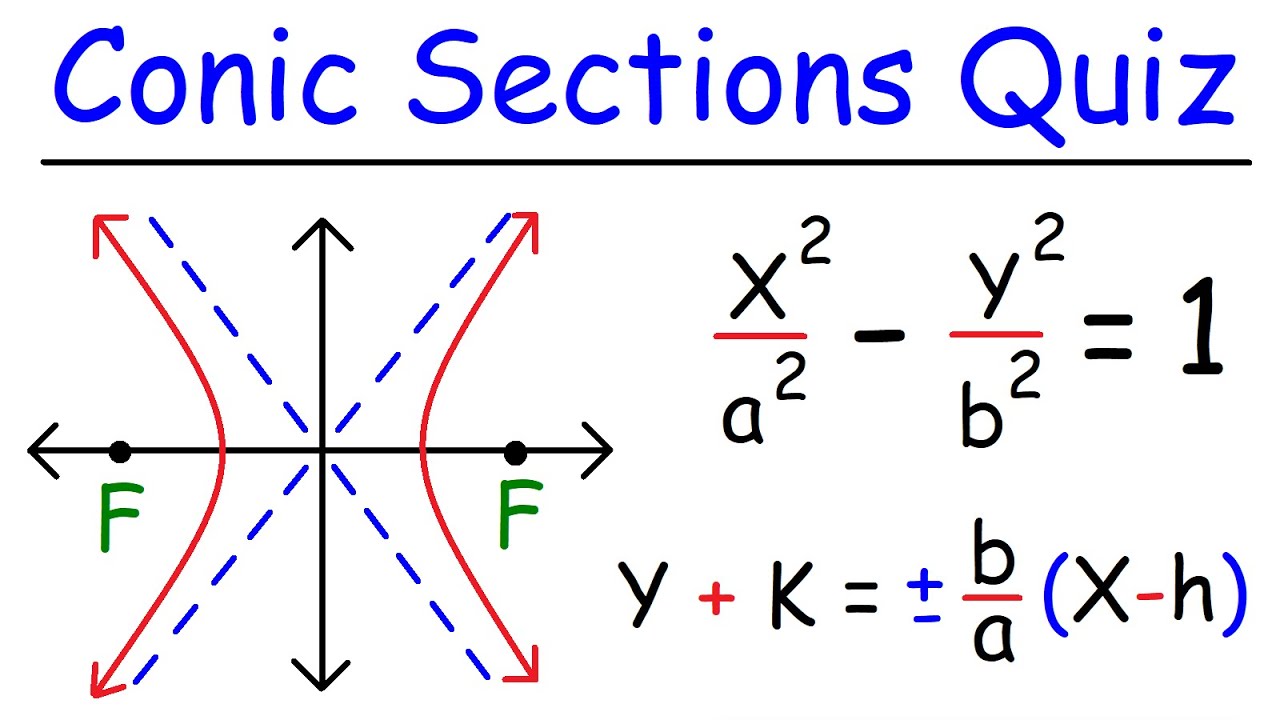
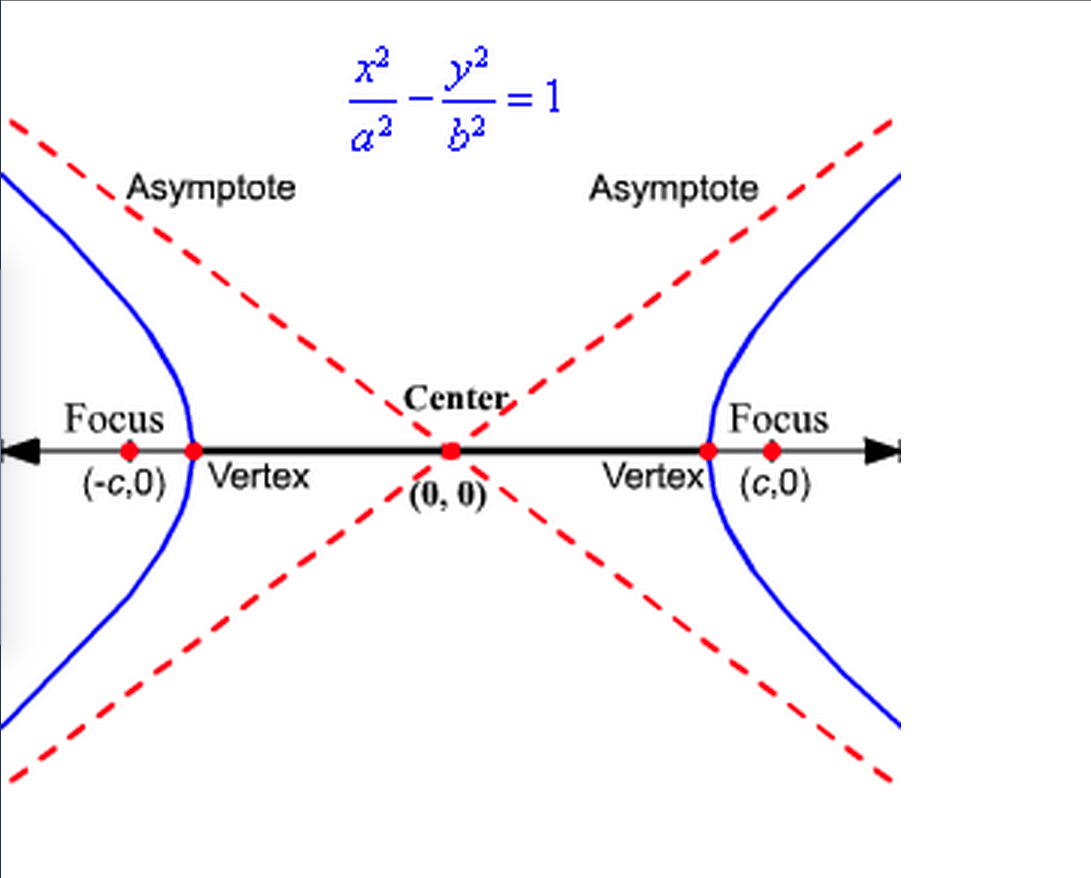
The main difference is that for the ellipse, a2 −c2 a 2 − c 2 is positive whereas for the hyperbola it is negative. A hyperbola’s eccentricity is constrained to e > 1 and has no upper bound. When we tilt the plane slightly, we get an ellipse.

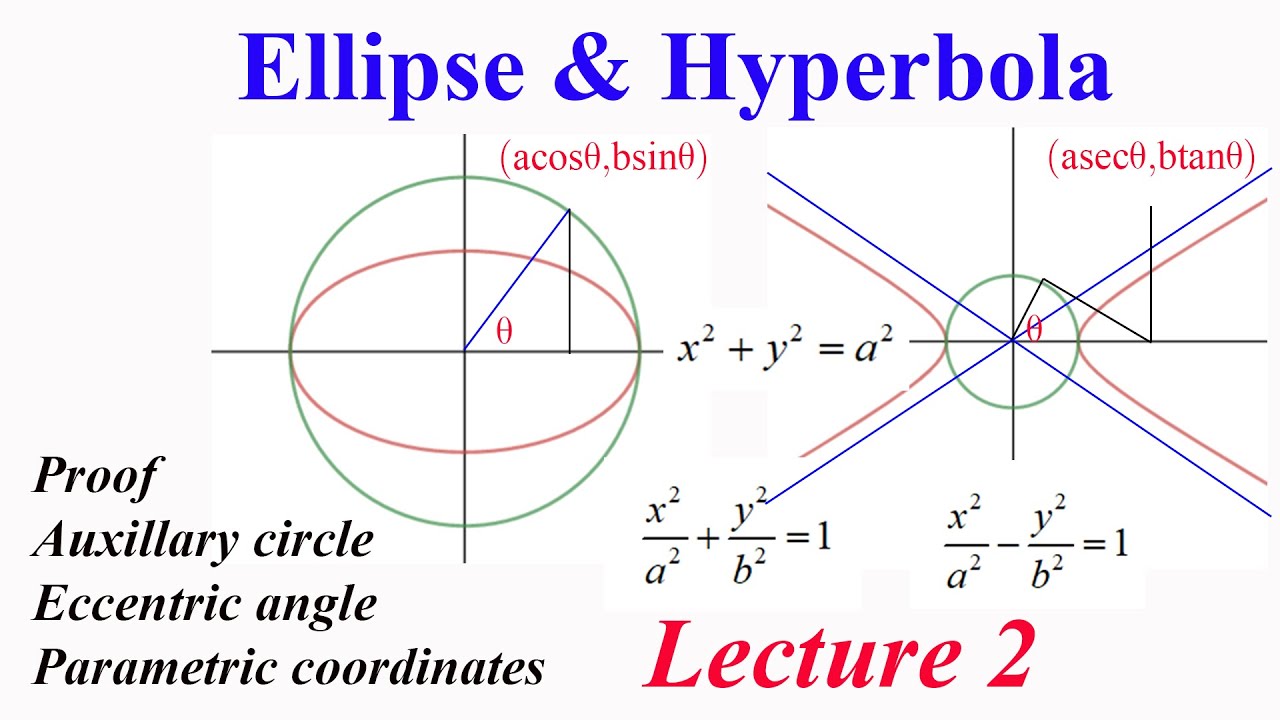
Notice that the definition of a hyperbola is very similar to that of an ellipse. If we tilt the plane a lot, we get a hyperbola. And you can do the same with ellipses, which are essentially the inverse of a hyperbola:

X^2/9 + y^2/4 = 1. Throughout mathematics, parabolas are on the border between ellipses and hyperbolas. The difference between parabola and hyperbola is the eccentricity of parabola is equal to 1 but eccentricity of hyperbola is greater than 1.

And if e>1, it is a hyperbola; The intersection of the asymptotes forms a centre. The obvious difference here is that for a hyperbola, the vertices are inside the foci;

Furthermore, hyperbolas (similar to ellipses) obey a fundamental rule regarding the distances. See a comparison of an ellipse vs. You give it an input value and you get an output value.

Find out what the foci of an ellipse are using an example. Why are these not functions? Each of the two branches bends around two focal points.

A parabola is generated when a plane intersects a cone parallel to the generating line. A hyperbola is the set of all points (x, y) (x, y) in a plane such that the difference of the distances between (x, y) (x, y) and the foci is a positive constant. A + b = const a + b = c o n s t.

A hyperbola's equation will result in asymptotes reflected across the x and y axis, while the ellipse's equation will not. Suppose, the angle formed between the surface of the cone and its axis is β and the angle formed between the cutting plane and the axis is α, the eccentricity is; True, the latter two fail the vertical line test, but so what?

Learn about the foci of hyperbola and the foci of an ellipse. Econd degree curves include x2, xy, y2. If e=1, the conic is a parabola;