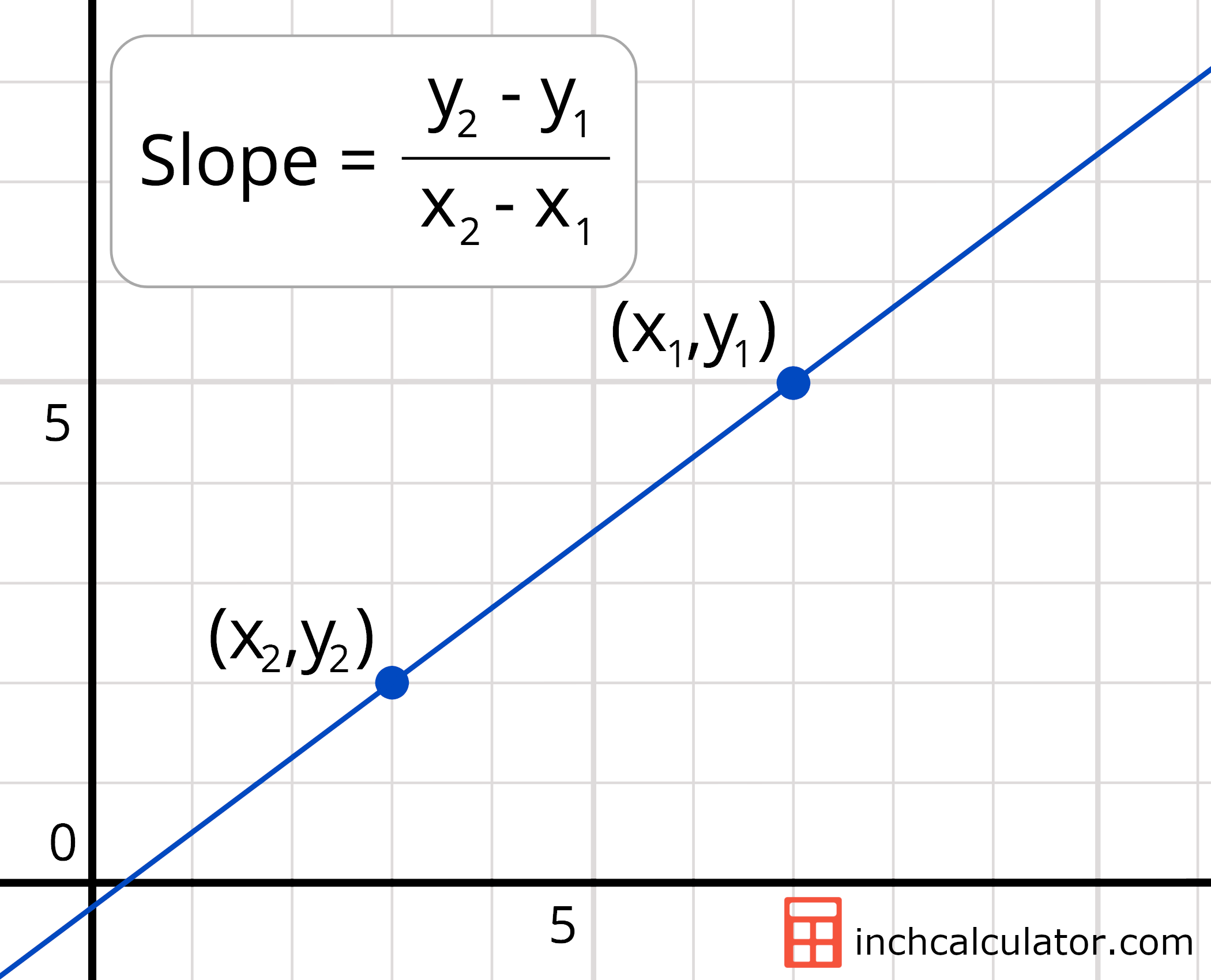Top Notch Tips About Can A Curved Line Have Slope Parallel Lines On Graph

In this article, we will look at the slope of a straight line, and see how this concept can be applied to a curve.

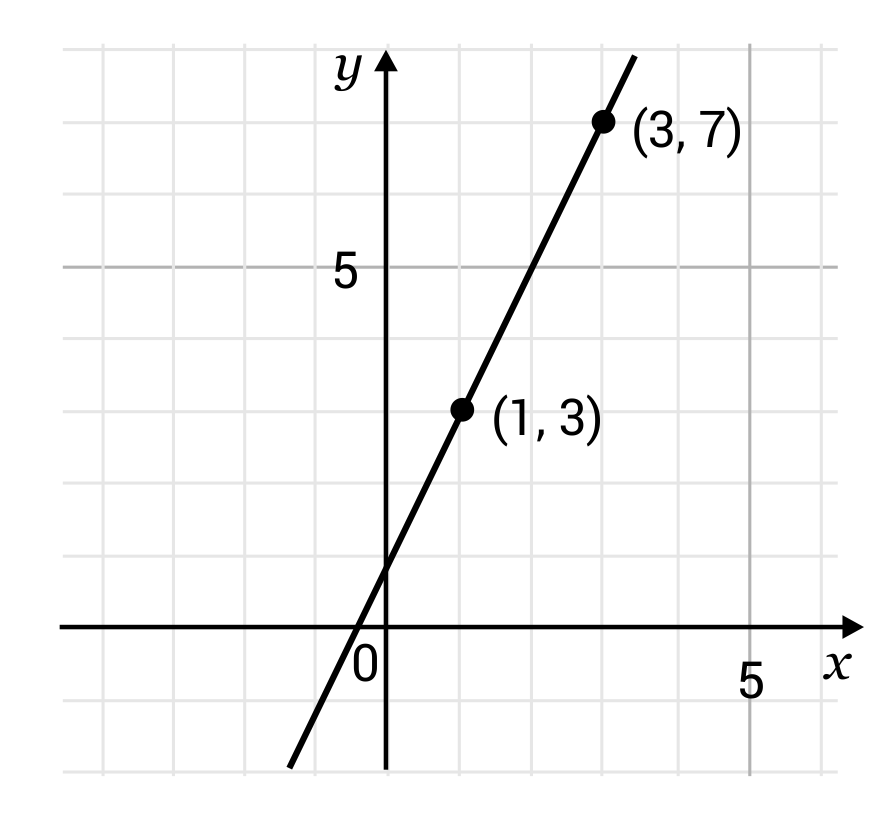
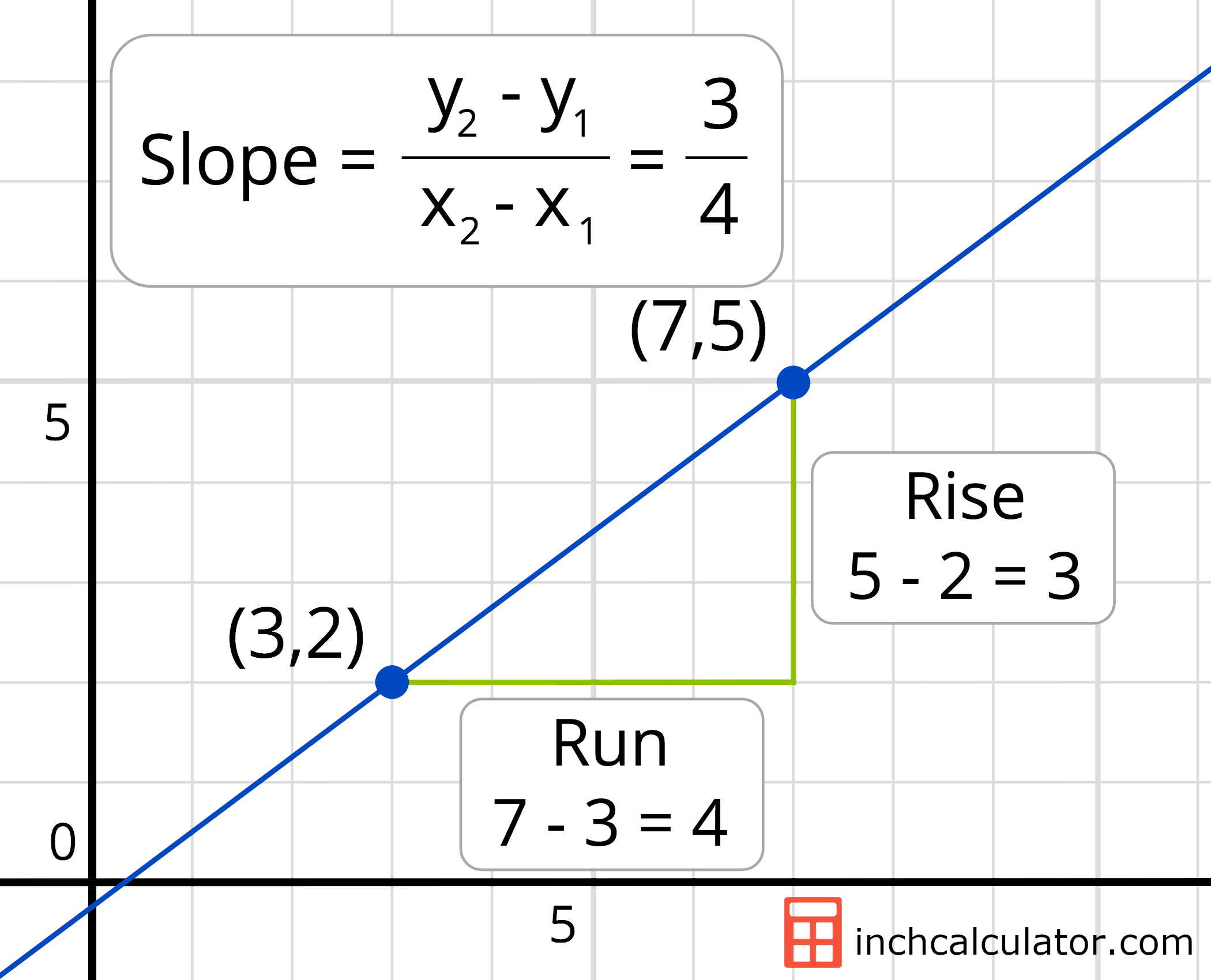
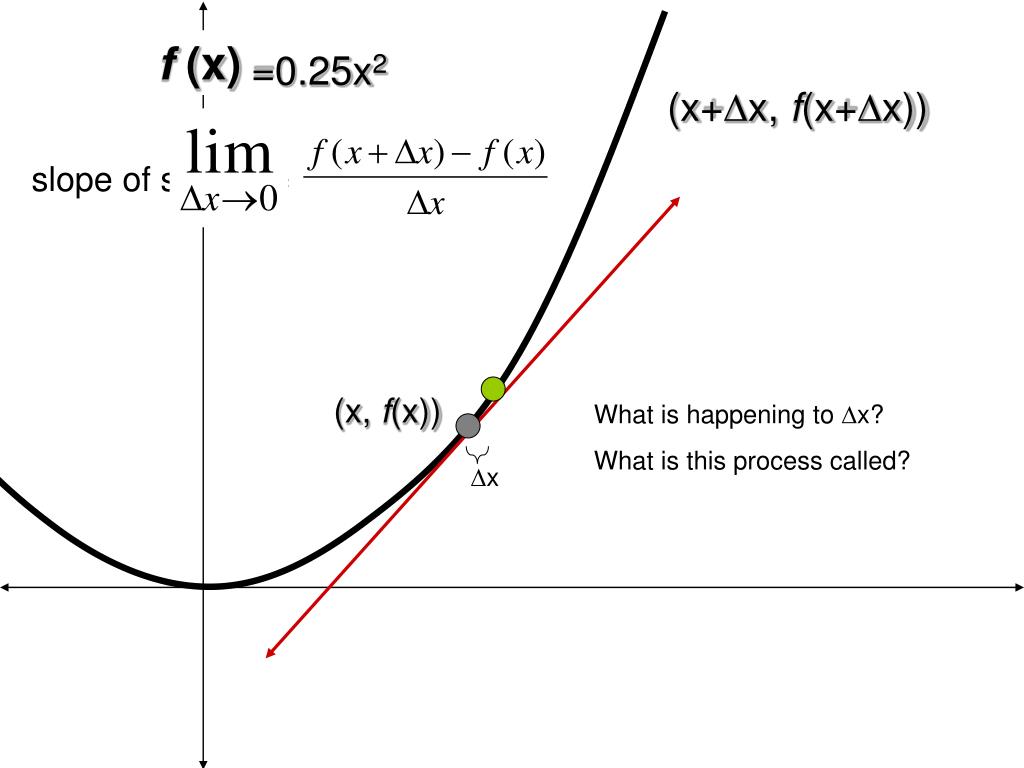
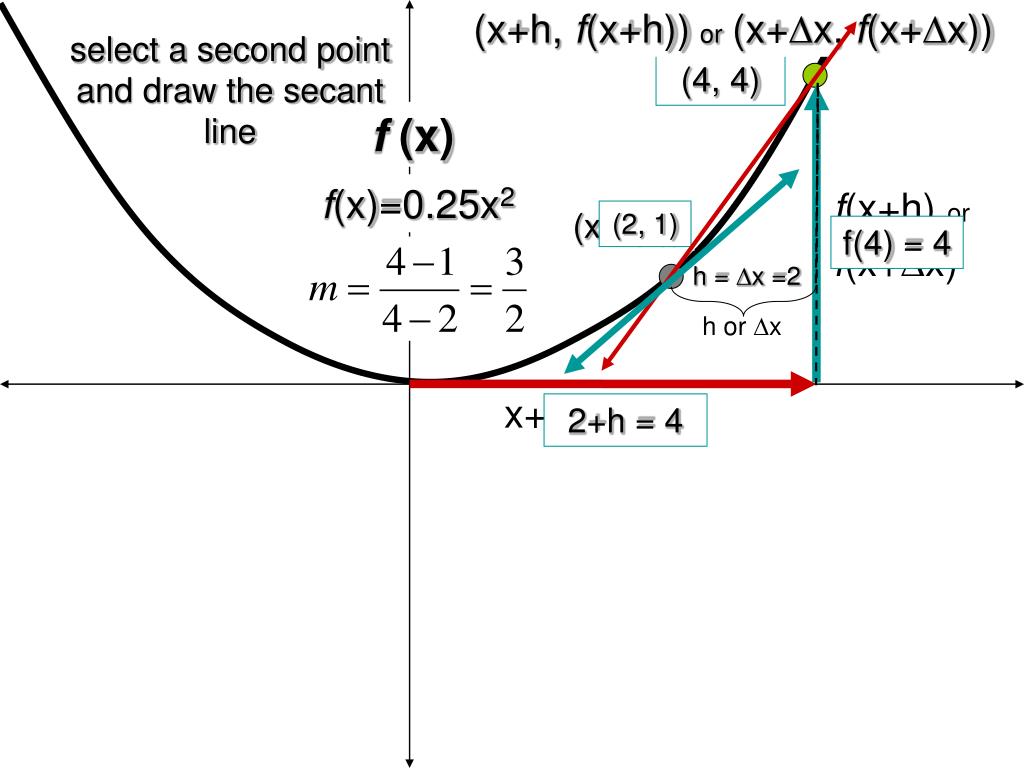
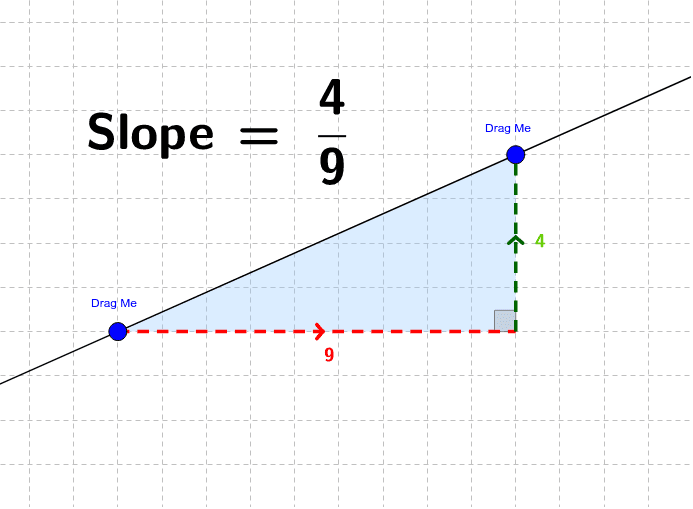
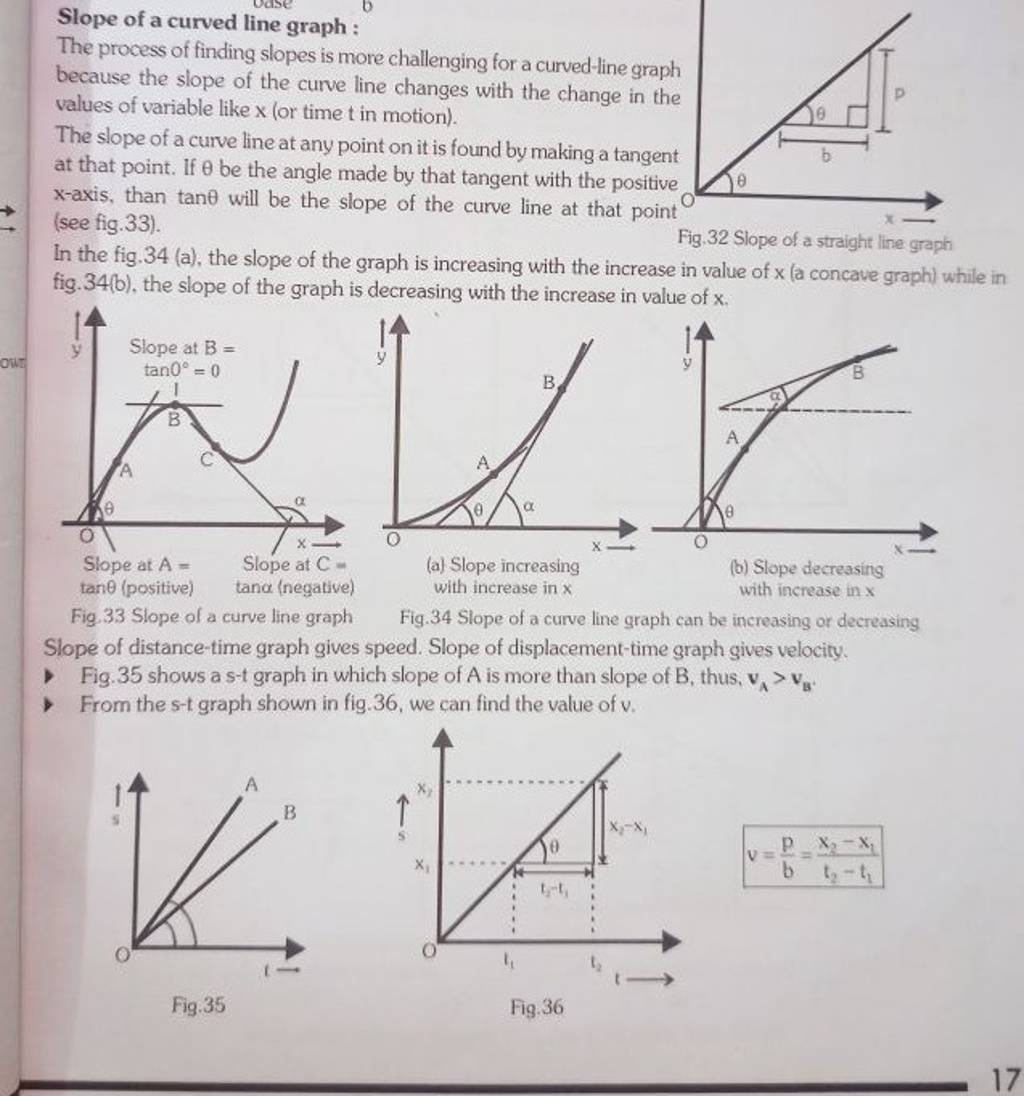
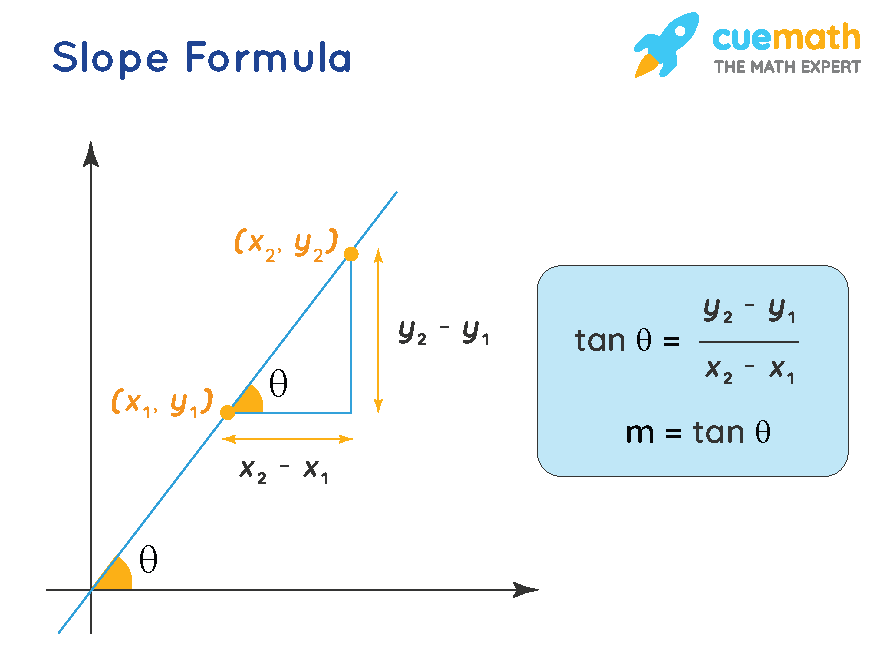
Can a curved line have a slope. For a curve that is not a straight line the slope of the curve at a specific point is the slope of the tangent line at that point. The slope of a line of a line is \(m = \frac{\text{rise}}{\text{run}}\). Discover the slope formula and learn how to find slope with two points.

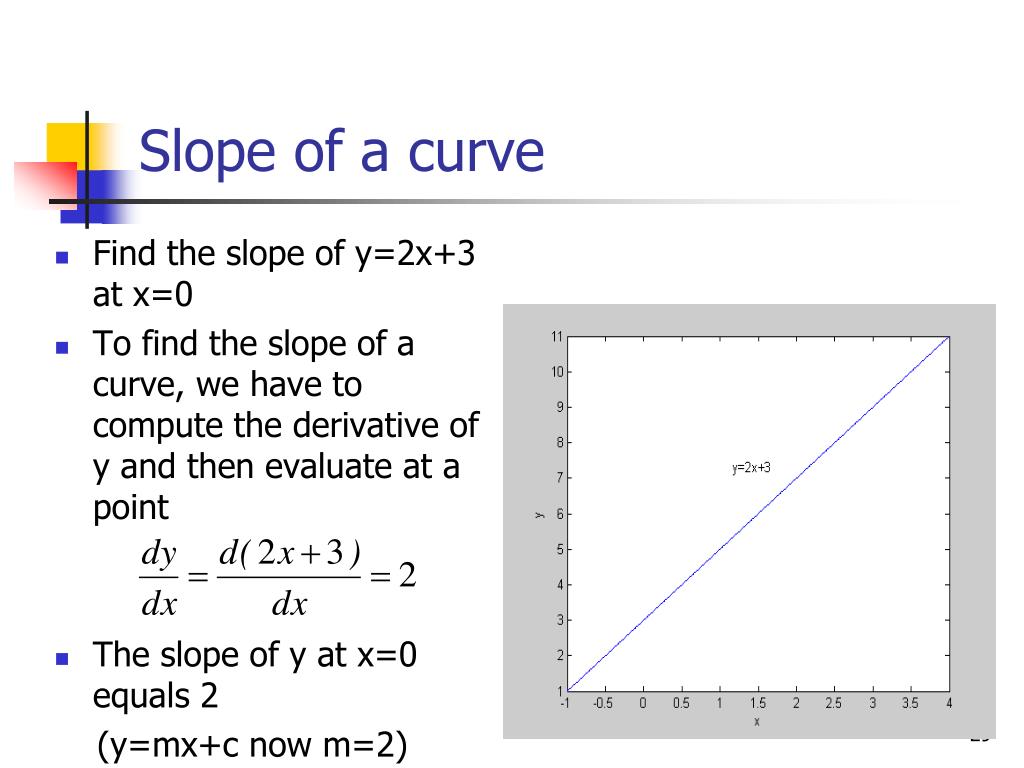
Slope of a curve using derivative. It is also defined as the instantaneous change occurs in the graph with the very minor increment of x. When dealing with a curved line, where the slope is changing, you can’t use the same formula.

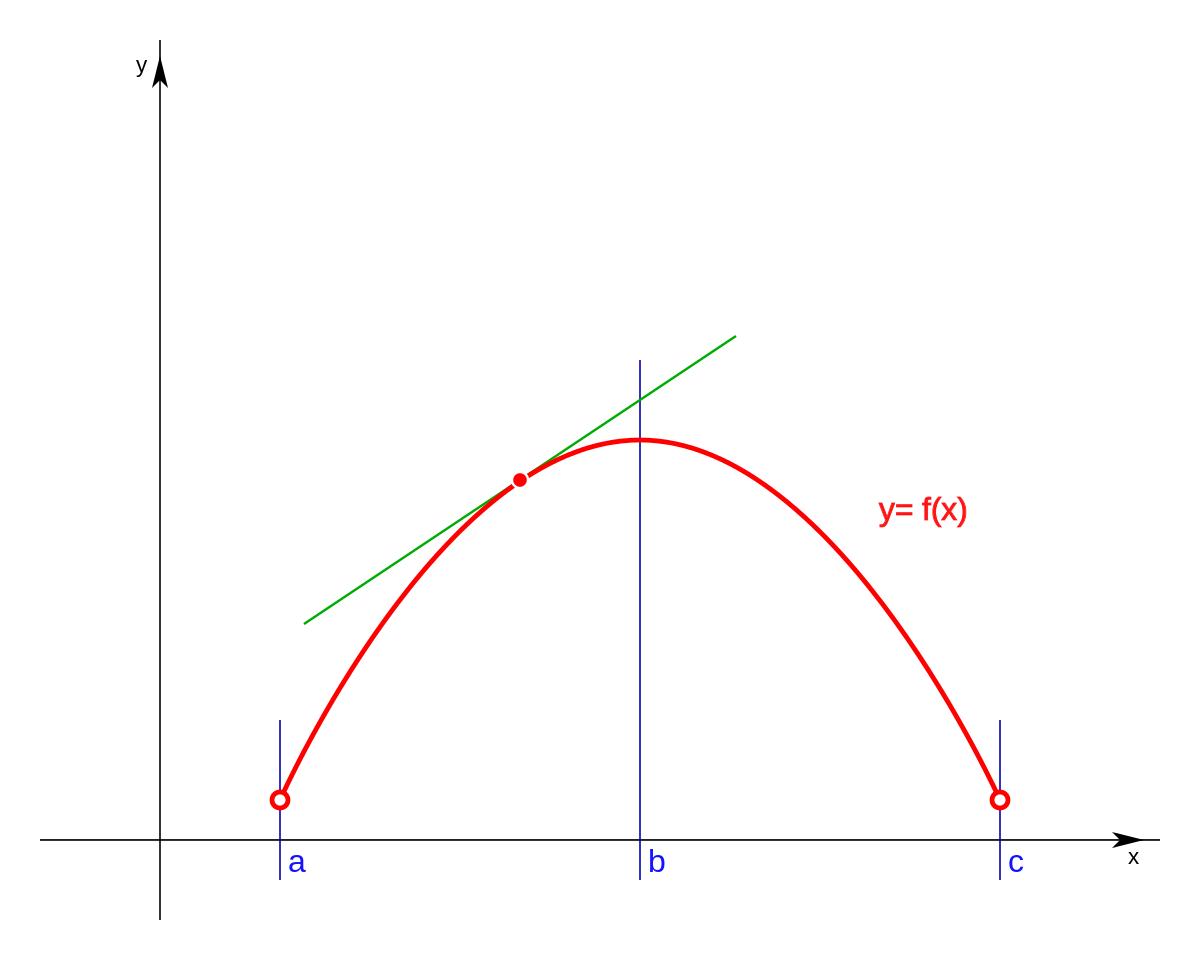
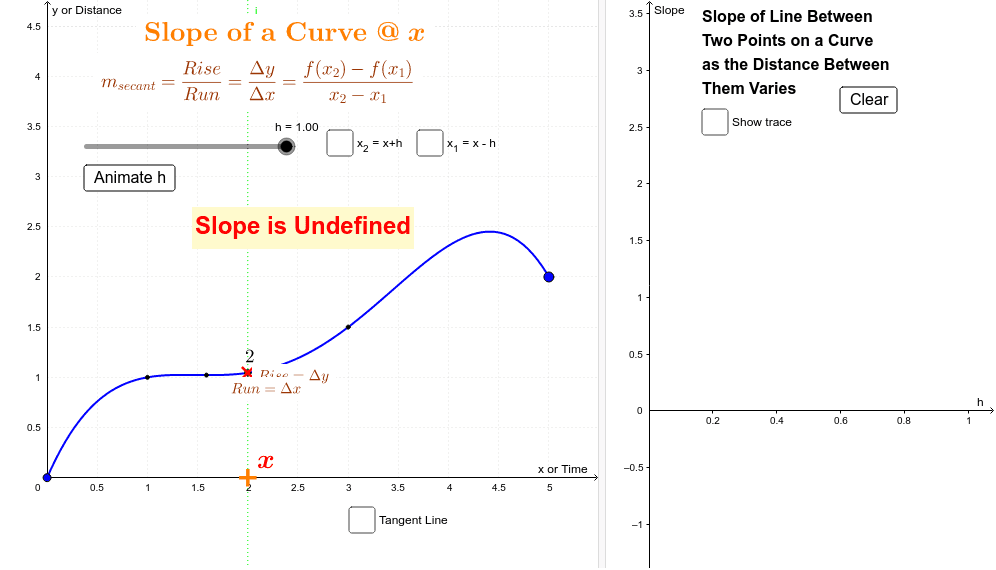
The slope of a line is a measure of how fast it is changing. The curvey path drops lower than the straight path, initially, which increases the speed at which it travels the majority of the distance. It does not have a slope per se, it only has an instantaneous slope at a given point (a line that is tangent to the point on the curve).

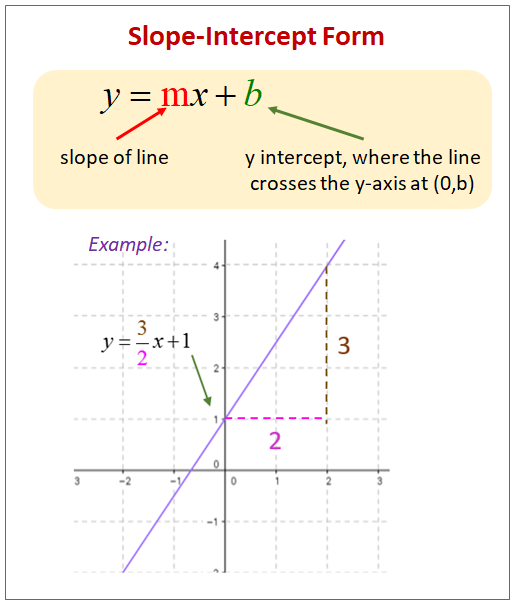
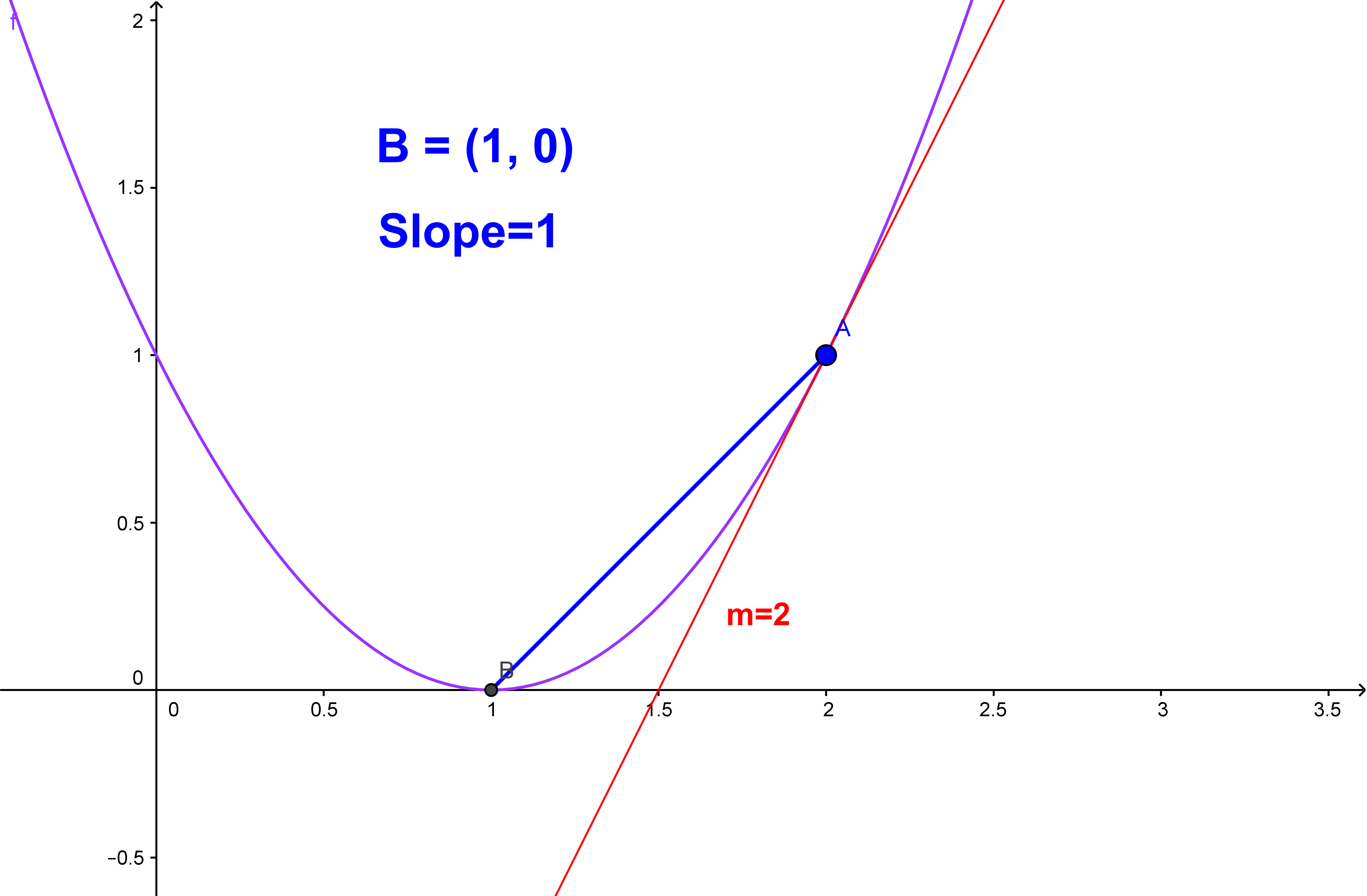
If the given curve is \(y=f(x),\) we evaluate \(\dfrac { dy }{ dx } \) or \(f'(x)\) and substitute the value of \(x\) to find the slope. A straight line maintains a constant slope, while a curved line has a varying slope. F' is the notation for the first derivative of the function f.

The slope of a curve at a point is equal to the slope of the tangent line at that point. Substitute the given value of x into the derivative dy/dx. The straight path drops only slightly, so the ball has to travel the majority of the distance at a lower speed.

The following steps would be useful to find the slope of the curve at some value of x. The rise measures the vertical change and the run measures the horizontal change between two points on the line. Generalizing this, differential calculus defines the slope of a curve at a point as the slope of its tangent line at that point.

When the curve is approximated by a series of points, the slope of the curve may be approximated by the slope of. Moreover, the 'intuitive' concept of a tangent line isn't all that convincing when you take a step back and think about it. The top diagram at the right is the graph of y = 2 x and the slope of this graph at the point (0,1) is the slope of the tangent line at (0,1).

There are two common formulas for slope: Calculate the slope of a line through two given points using the slope calculator. Colon expected (click for details)

The slope of a line is a measure of its steepness. Math and physics tutor. This is a problem made for calculus though.

To find the slope at a point along a curved line, you find the first derivative of the function and evaluate it at that point. M = change in y/change in x But enough about theory, let’s take a look at how we can actually find slope of a curve (or slope of a tangent of a curve).