Awesome Info About Is Smooth The Same As Continuous Secondary Axis Data Studio

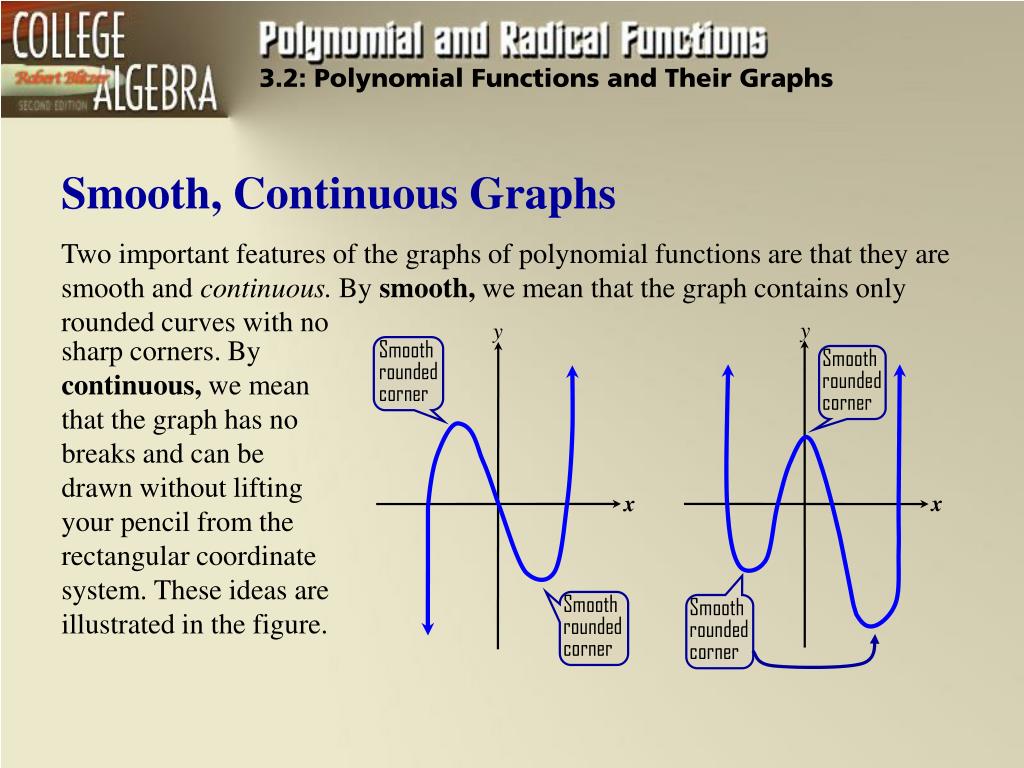
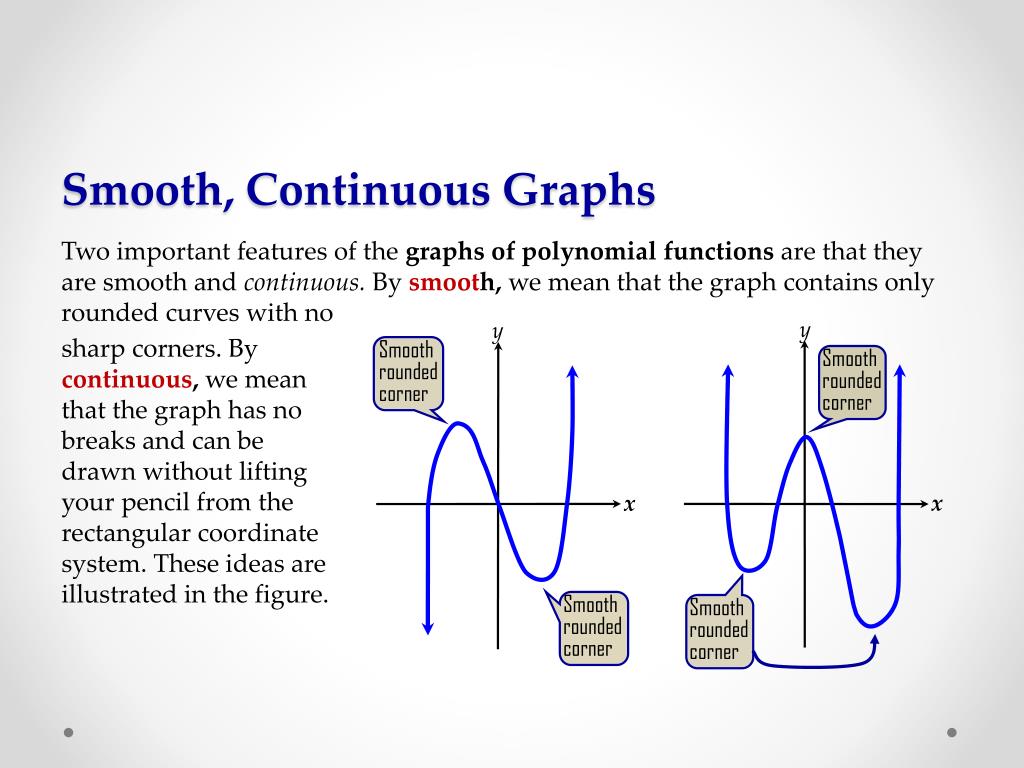
The graph can be drawn without lifting the pen from the paper.

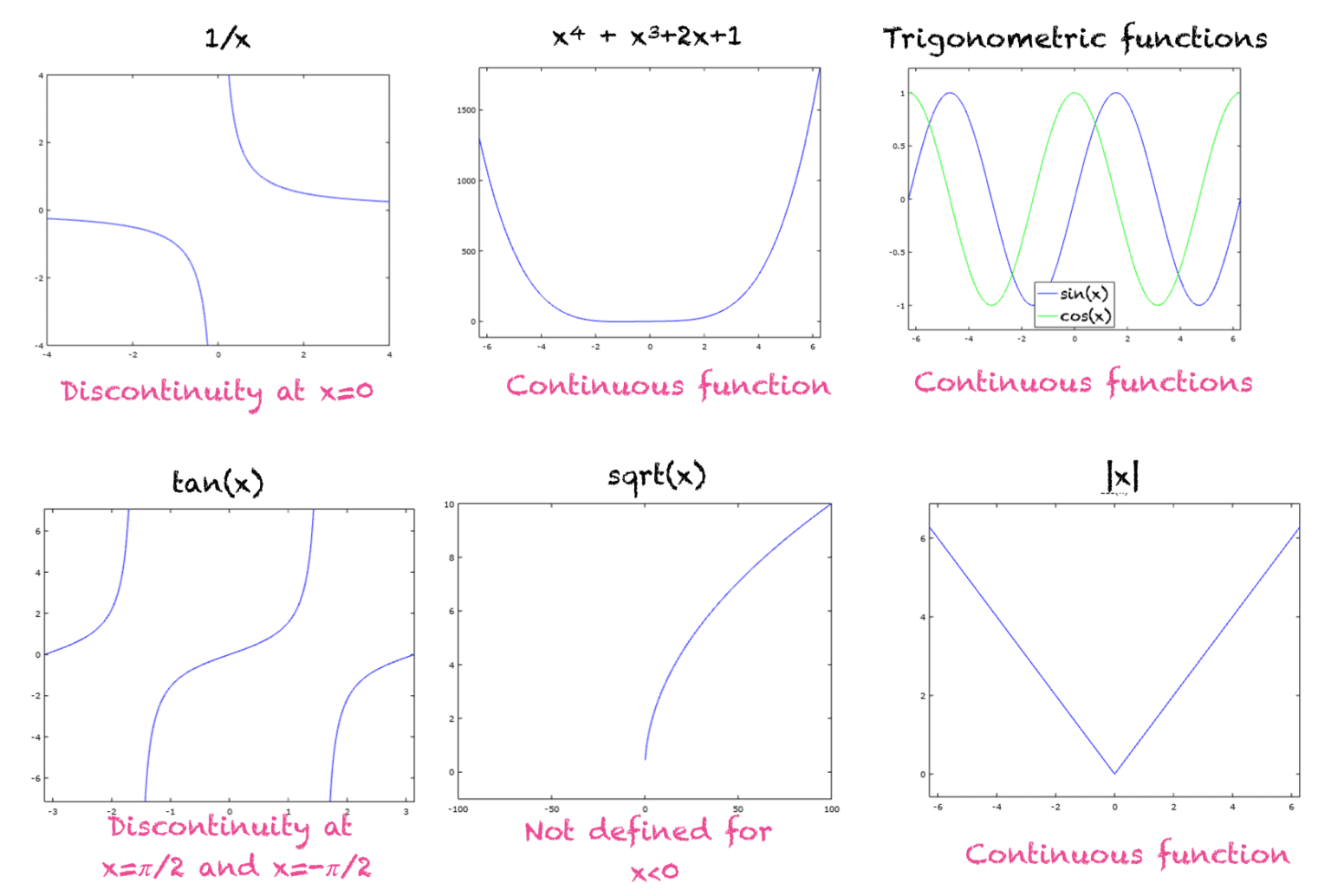
Is smooth the same as continuous. A smooth curve is a graph that has no sharp corners. Smoothness, like continuity, is a local condition: A continuous function has no breaks in its graph:

M \to n$ be a smooth map. The more we smooth, the more high frequency components we kill. A smooth function is a function that has continuous derivatives up to some desired order over some domain.

Find values of the constants a and b for which the following function is contin uous but not differentiable. Most simply, any discontinuous function is not smooth at any input where a discontinuity occurs. A smooth function has continuous derivatives, up to some specified order.

But even the continuous ramp function is not smooth at the start. A function for which each value of the argument is a smooth point (cf. A function of class is a function of smoothness at least k;

Piecewise smooth functions are continuous with a finite number of continuous derivatives, while piecewise continuous functions may have a finite number. By zooming in, it seems. In fact, attenuating high frequency components of a signal can be taken to be the definition of smoothing.

Continuous but not smooth. We can say that it is $c_n$, smooth to second order, or twice differentiable. Sin 2x, x ≤ 0.

Given an open subset u m, we say that a function. The general rule is that you would use an isotropic smooth s(x, cov1) if x and cov1 had the same units and you would use an anisotropic smooth te(x, cov1) if x. A smooth function can be discontinuous.

2 we say that smooth on some open. Since it is discontinuous at any point, it naturally cannot be smooth, or any of the other options. To see if we can translate this into more mathematical terms, we'll focus on.

F(x) = ax + b, x > 0; A function can therefore be said to be smooth over a. Smooth usually means no rough edges or corners.

One particularly useful class of smooth functions is. Smooth point of a function). Let $m$ and $n$ be smooth manifolds of dimensions $m$ and $n$, respectively, and let $\phi :