Fun Tips About What Is The Slope Of A Horizontal Line Best Fit Google Sheets How To Make Graph

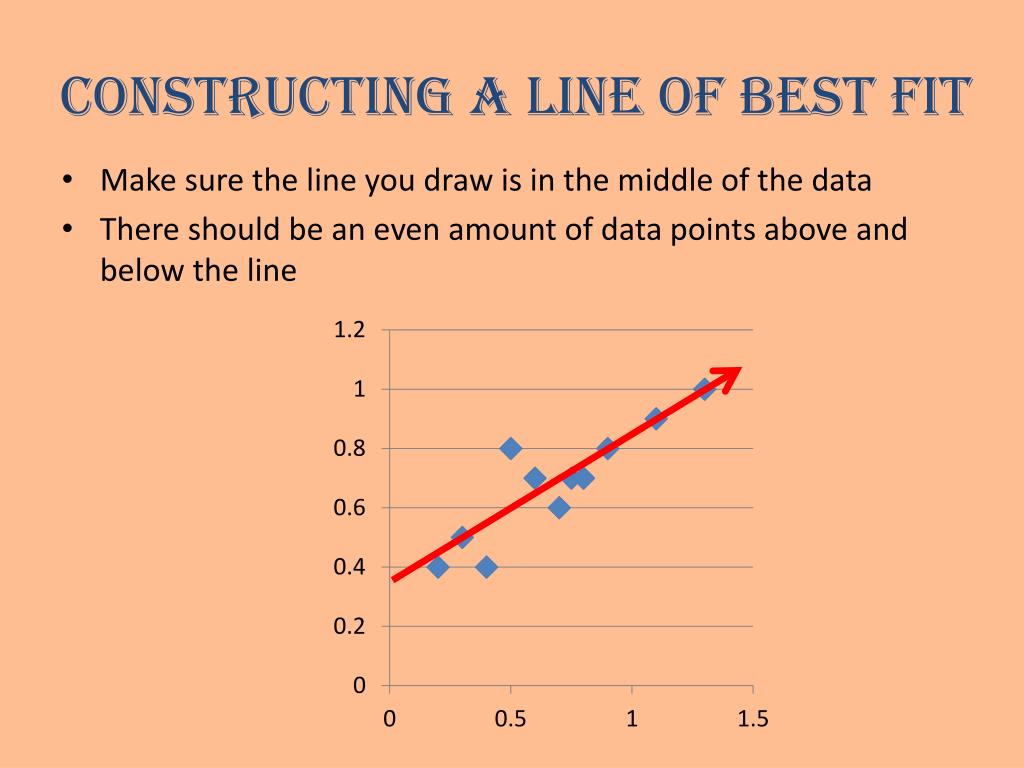
The term “best fit” means that the line is as close to all points (with each.

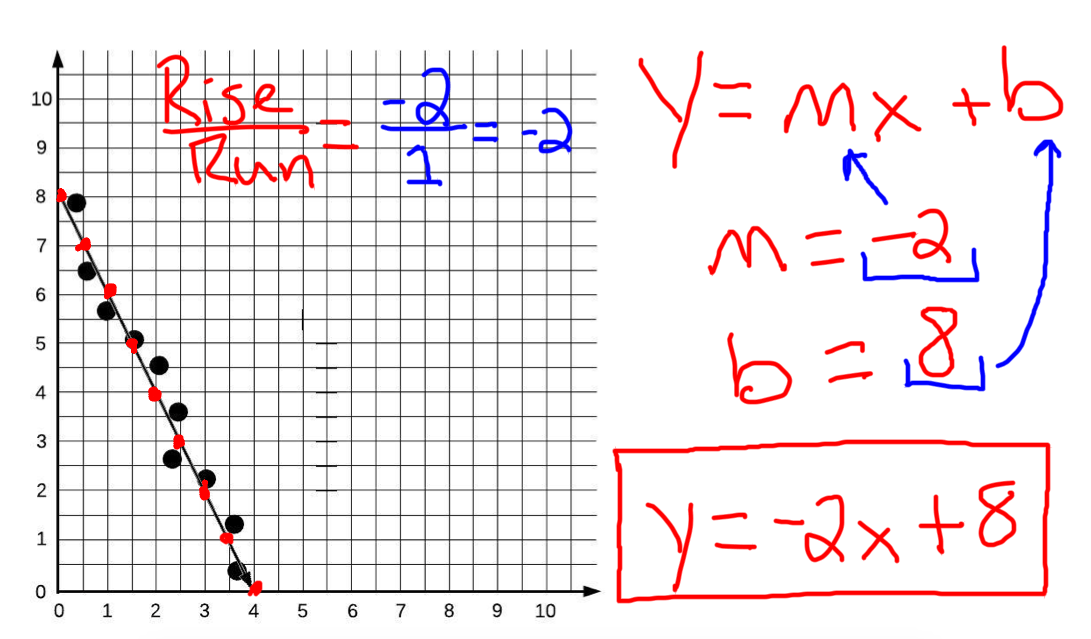
What is the slope of a horizontal line of best fit. The criteria for the best fit line is that the sum of the squared errors (sse) is minimized, that is, made as small as possible. Slope of the line of best fit represents the rate of change between the two variables. Instead, the idea is to get a.

Y ^ = 2.5 x + 0.5. When i apply linear regression, i have. Describing linear relationships with correlation;

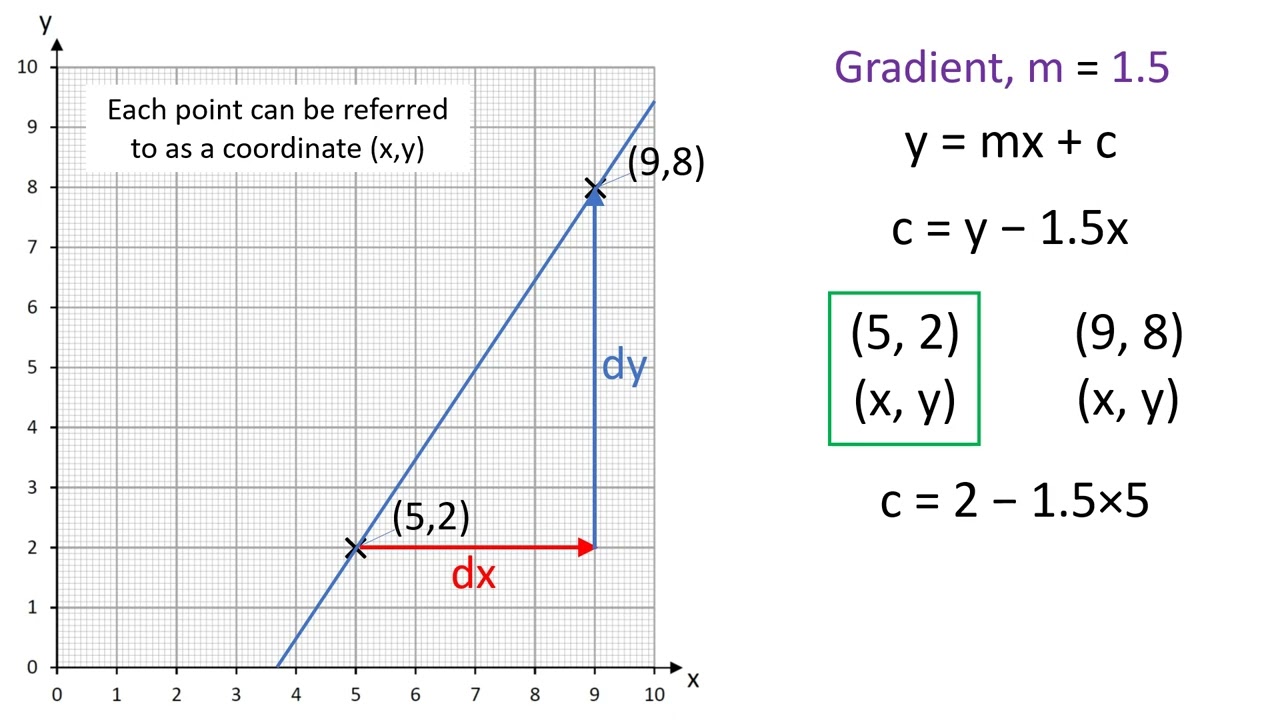
Any other line you might choose would have a higher. However, i'll show you a simplified version of the method to obtain an approximate line. The first thing to realize is that each solution is a point on the line.

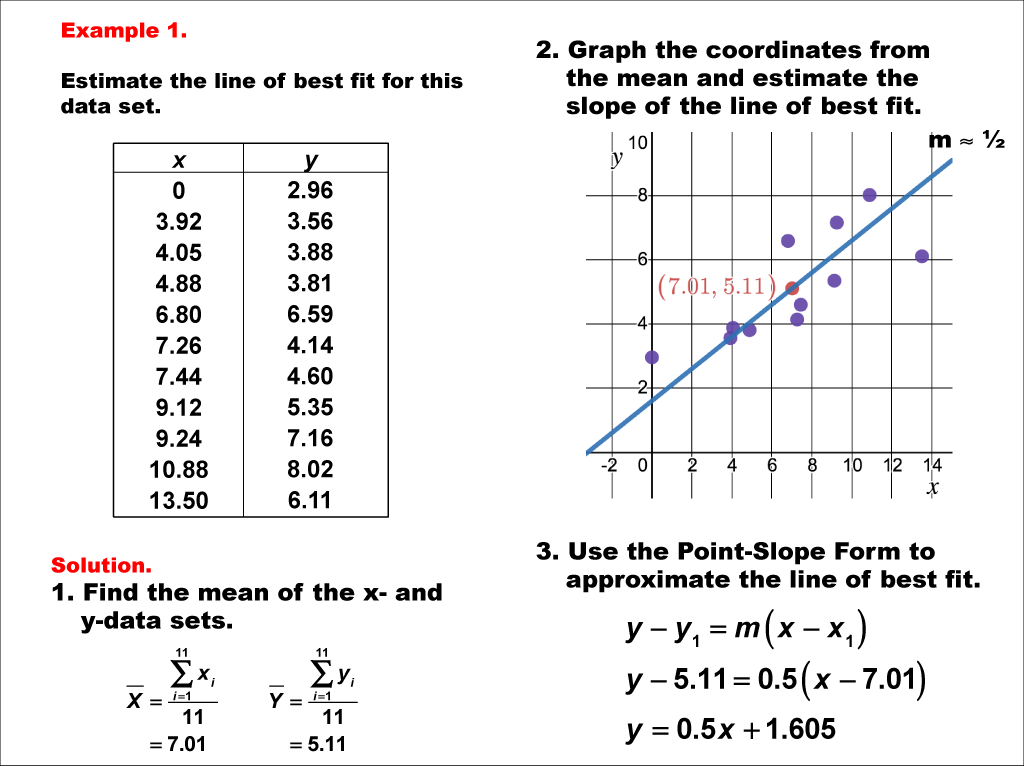
To find the line of best fit, we can use the least squares regression method. The least square method is the most. Substituting a = 0.458 and b = 1.52 into the equation y = ax + b gives us the equation of the line of best fit.

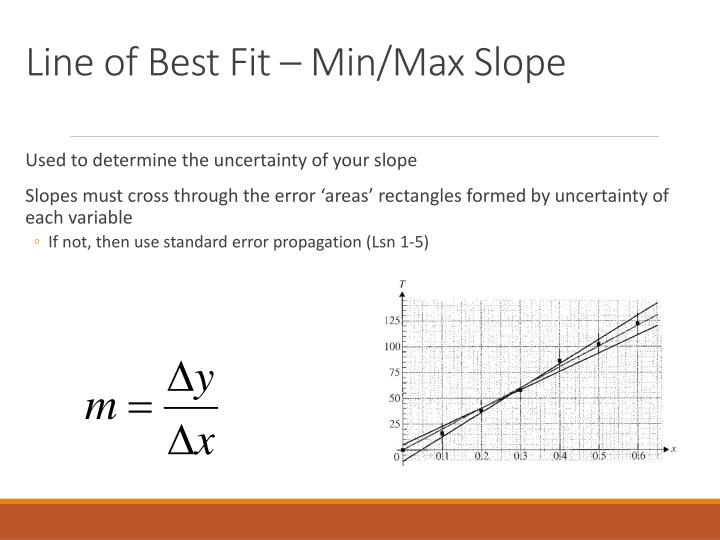
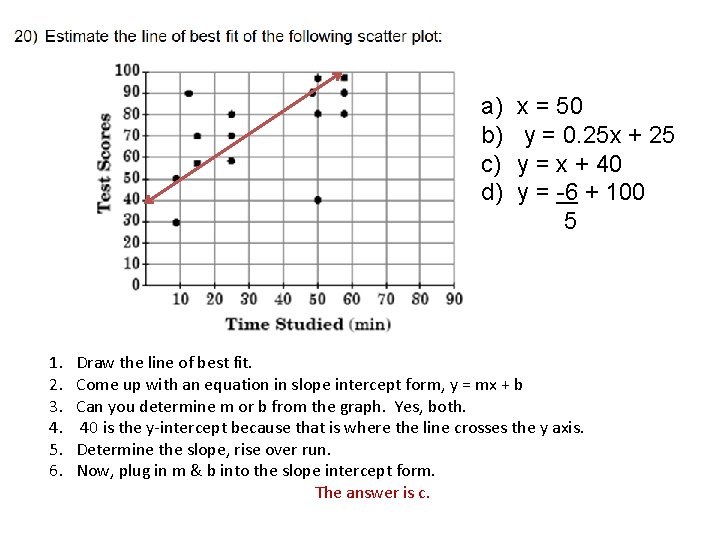
On a graph, we could try sketching a line. X = 12.7 y = 15.4. So, all we need to do.

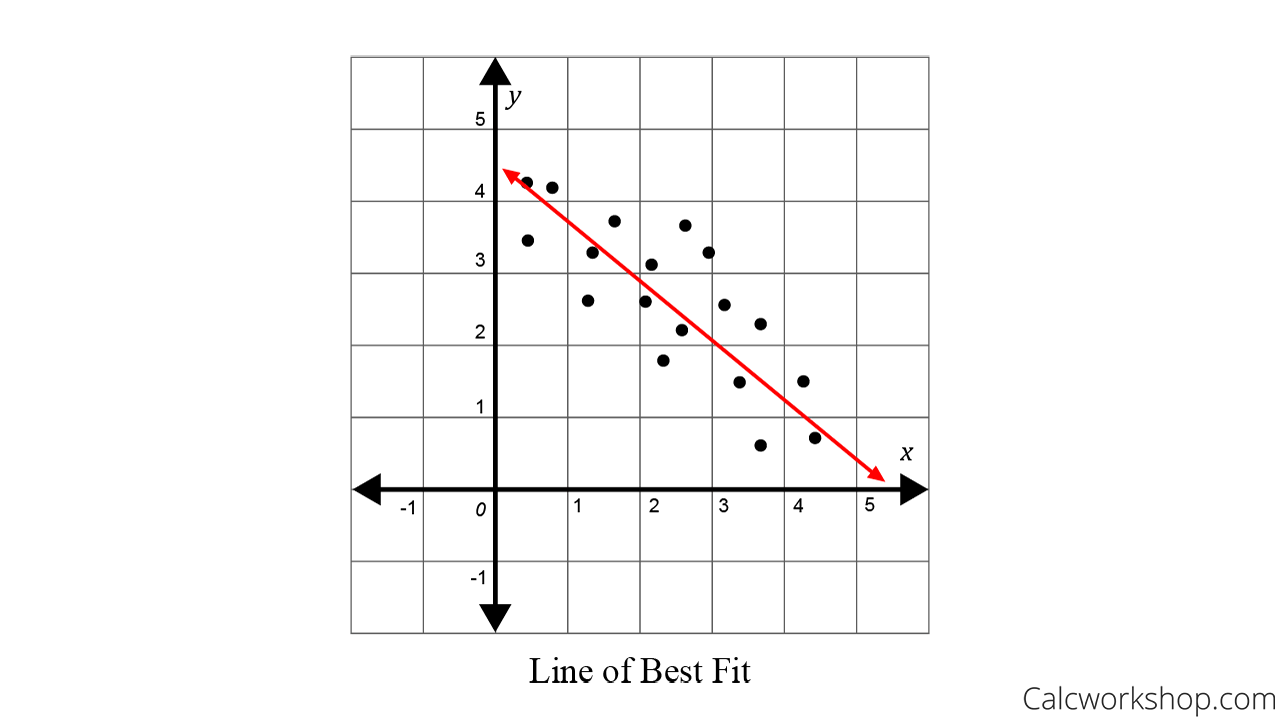
We will also see examples in this chapter where. In many cases, the line may not pass through very many of the plotted points. The closer the points are to the line of best fit the stronger the correlation is.

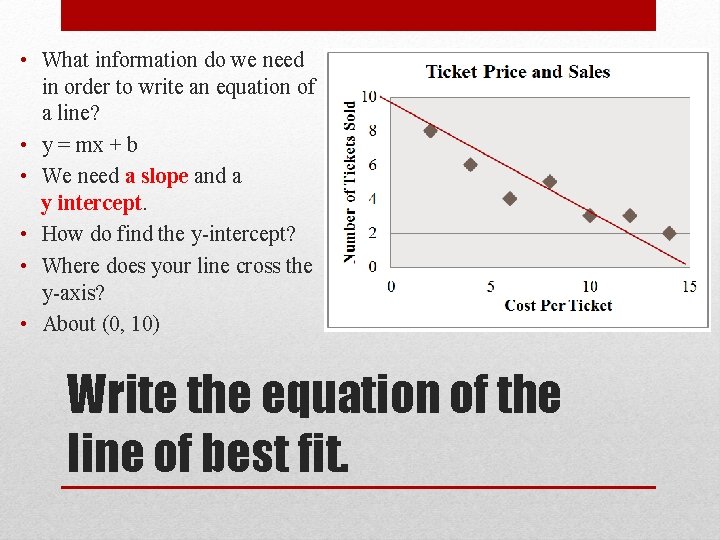
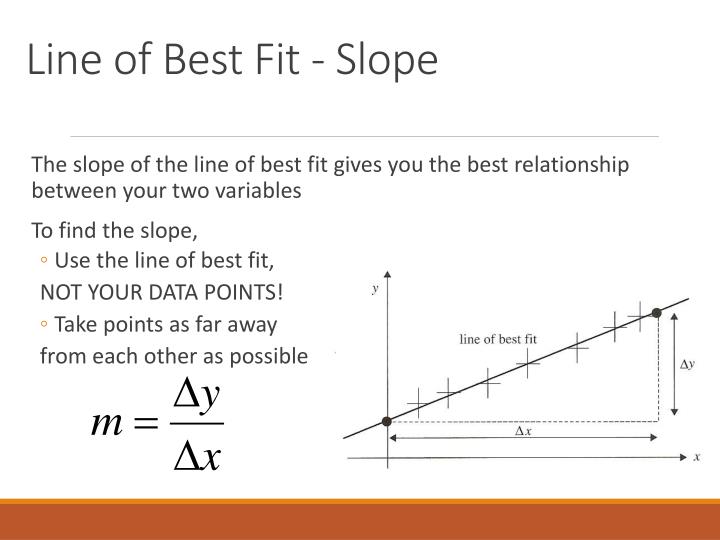
What does the slope of the line of best fit represent? Then drag the red line to find the line of best fit. You can determine the line of best fit by three methods:

I want to get a line of the best fit which is a line that passes as close as possible to a set of points defined by coordinates point_i = (x_i, y_i). Let's see how you did! Y ^ = 2.5 x − 0.5.

Y ^ = 2.5 x − 0.5. Fitting a line by eye residuals; Substituting a = 0.458 and b = 1.52 into the equation y = ax + b gives us the equation of the line of best fit.

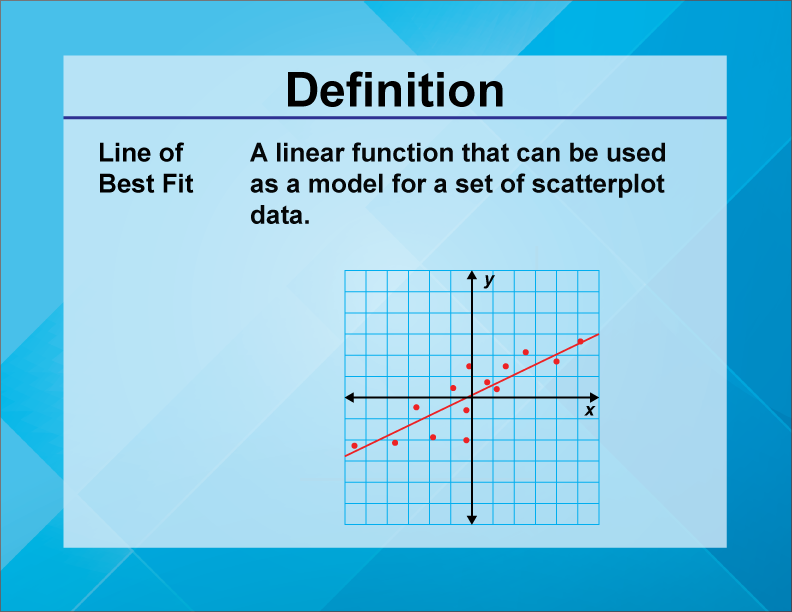
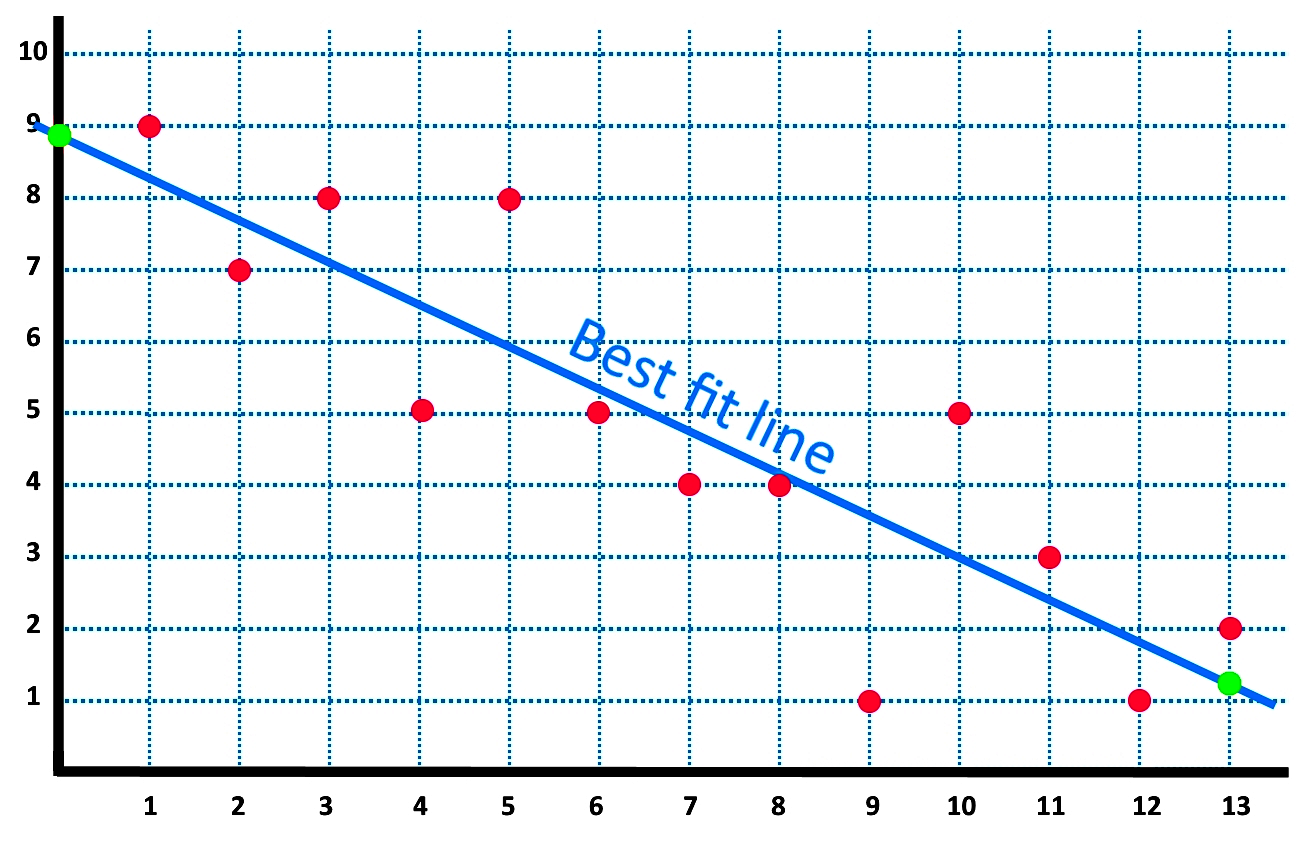
The 'line of best fit' is a line that goes roughly through the middle of all the scatter points on a graph. Y ^ = 2.5 x + 0.5. \ [y=0.458 x+1.52 \nonumber \] we can superimpose the plot of the line of best fit on our data set in two.