Breathtaking Info About Is Curve Positive Or Negative Horizontal Bar Type

The unemployment rate graph in figure 4, below, illustrates a common pattern of many line graphs:

Is curve positive or negative. Regarding negative areas, let's draw an analogy with a map. But it won't ever be negative. Despite the fact that the surface is two dimensional, the curvature is a scalar (i should say real) value at every point, not a vector.

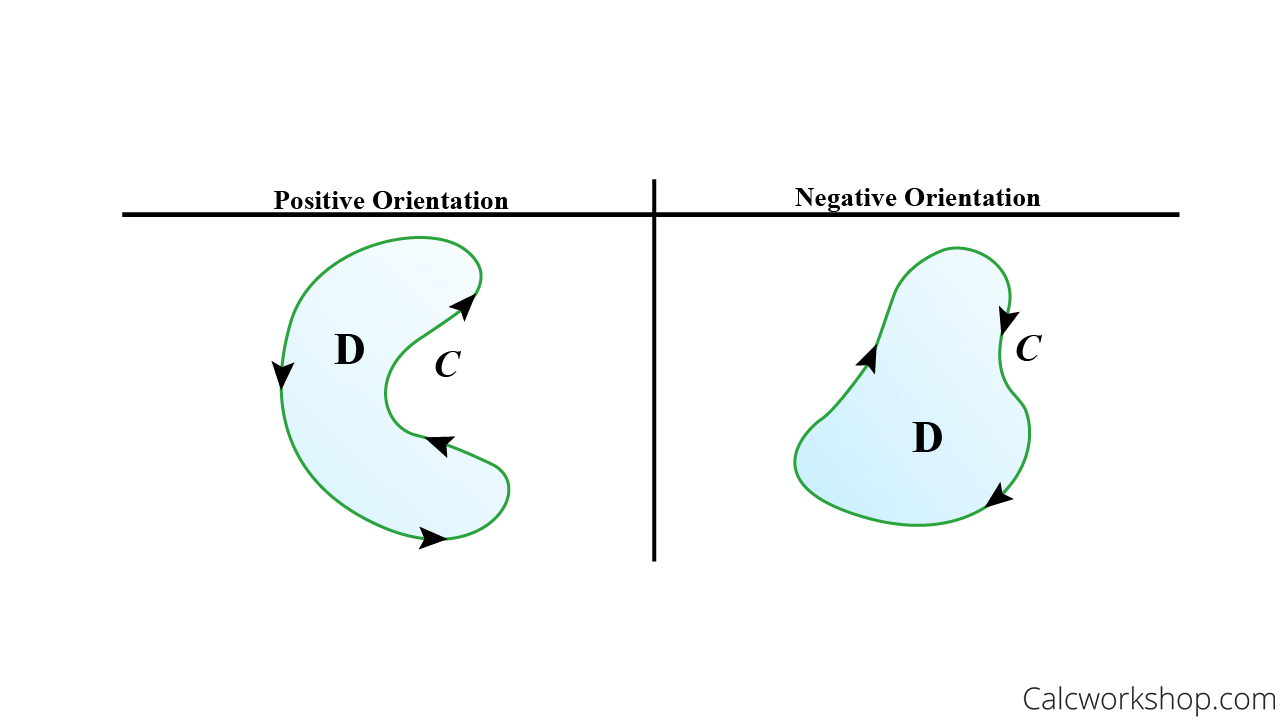
If the determinant is positive, the polygon is oriented counterclockwise. In general, a preference is convex if a convex combination of two bundles on the same indifference curve is preferred to those two bundles. If the determinant is negative, then the polygon is oriented clockwise.

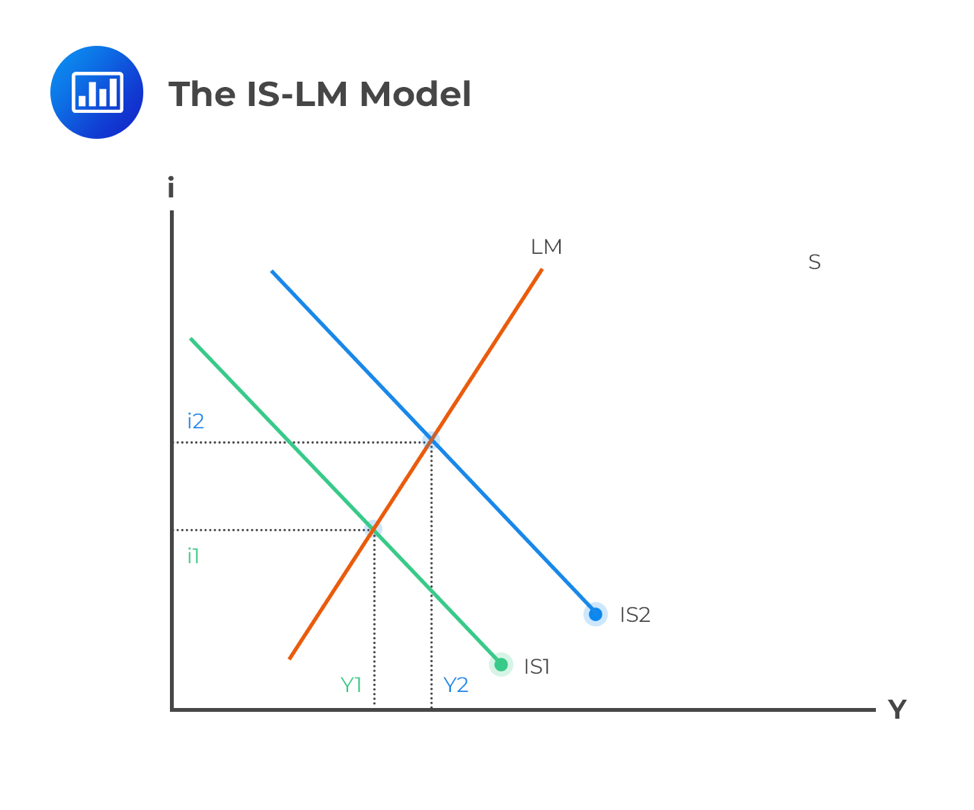
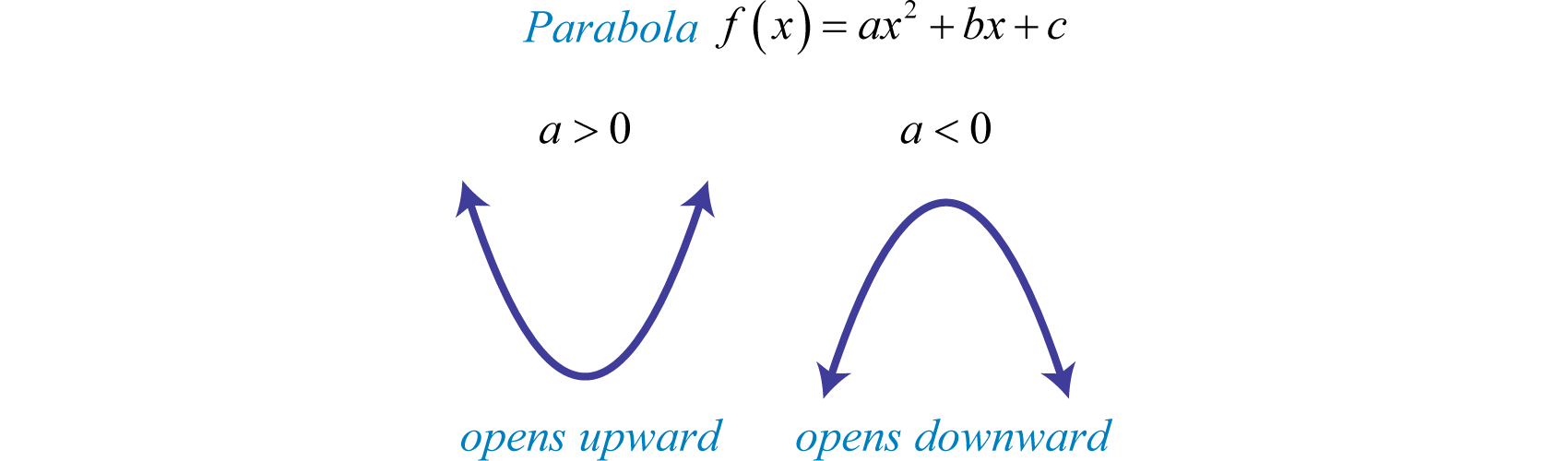
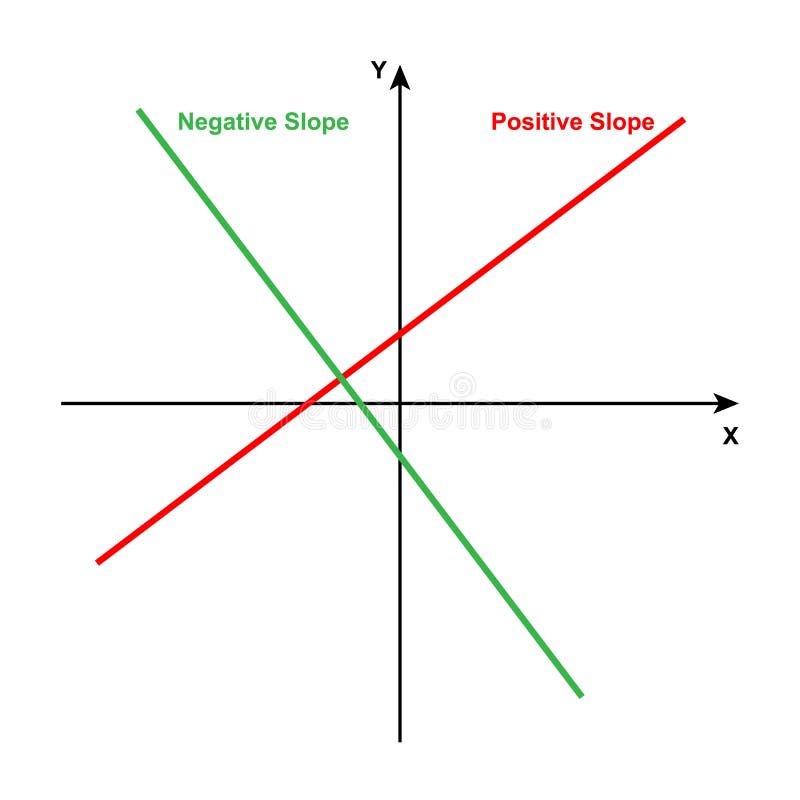
Some segments where the slope is positive, other segments where the slope is. The relationship between the real rates of interest and the corresponding equilibrium levels of the real output in the product market is called the is curve. Gradient is a measure of how steep a slope or a line is.

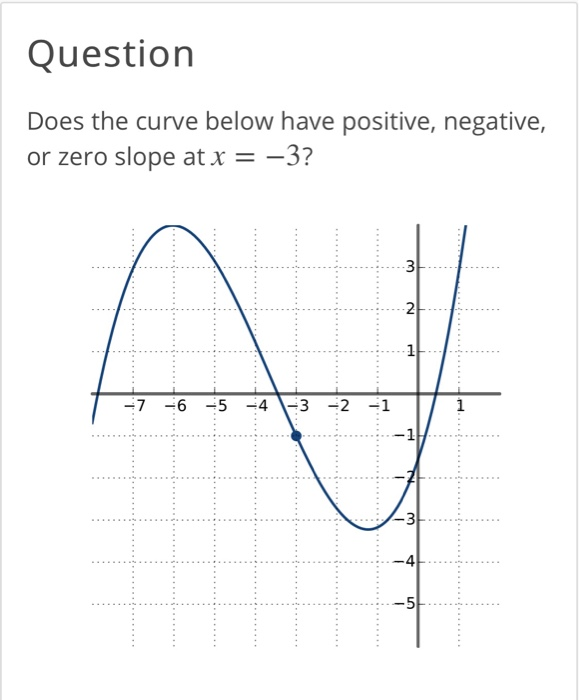
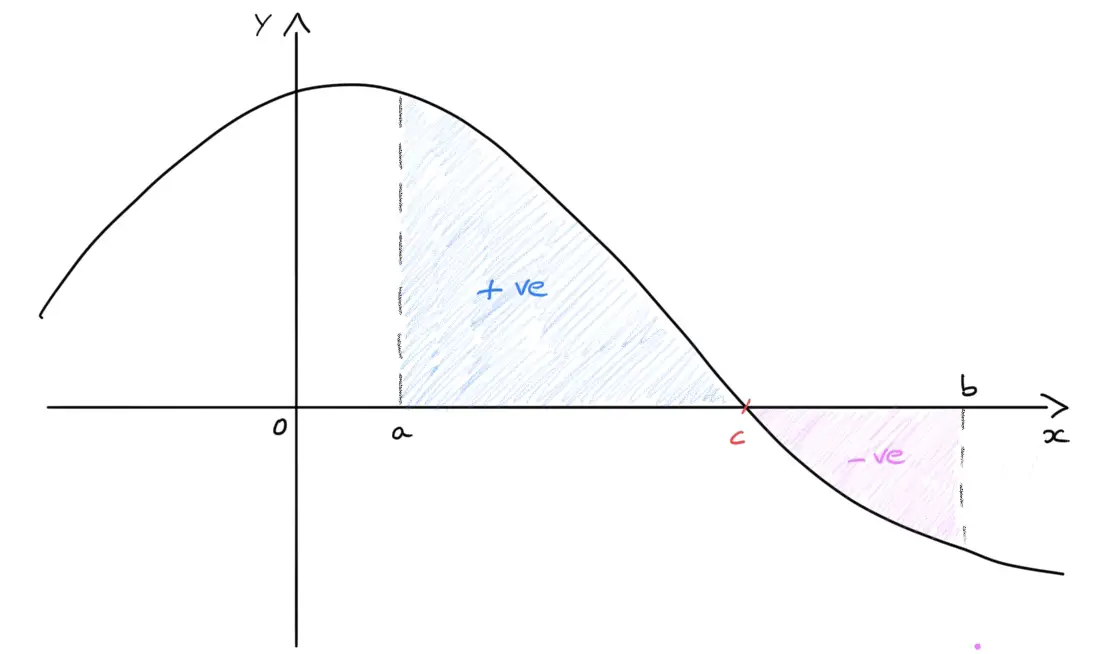
If you are integrating from 0 to 2*pi and getting a result of 0, then half of the area is positive and half of. In general, to determine if the slope of. Y increases as x increases.

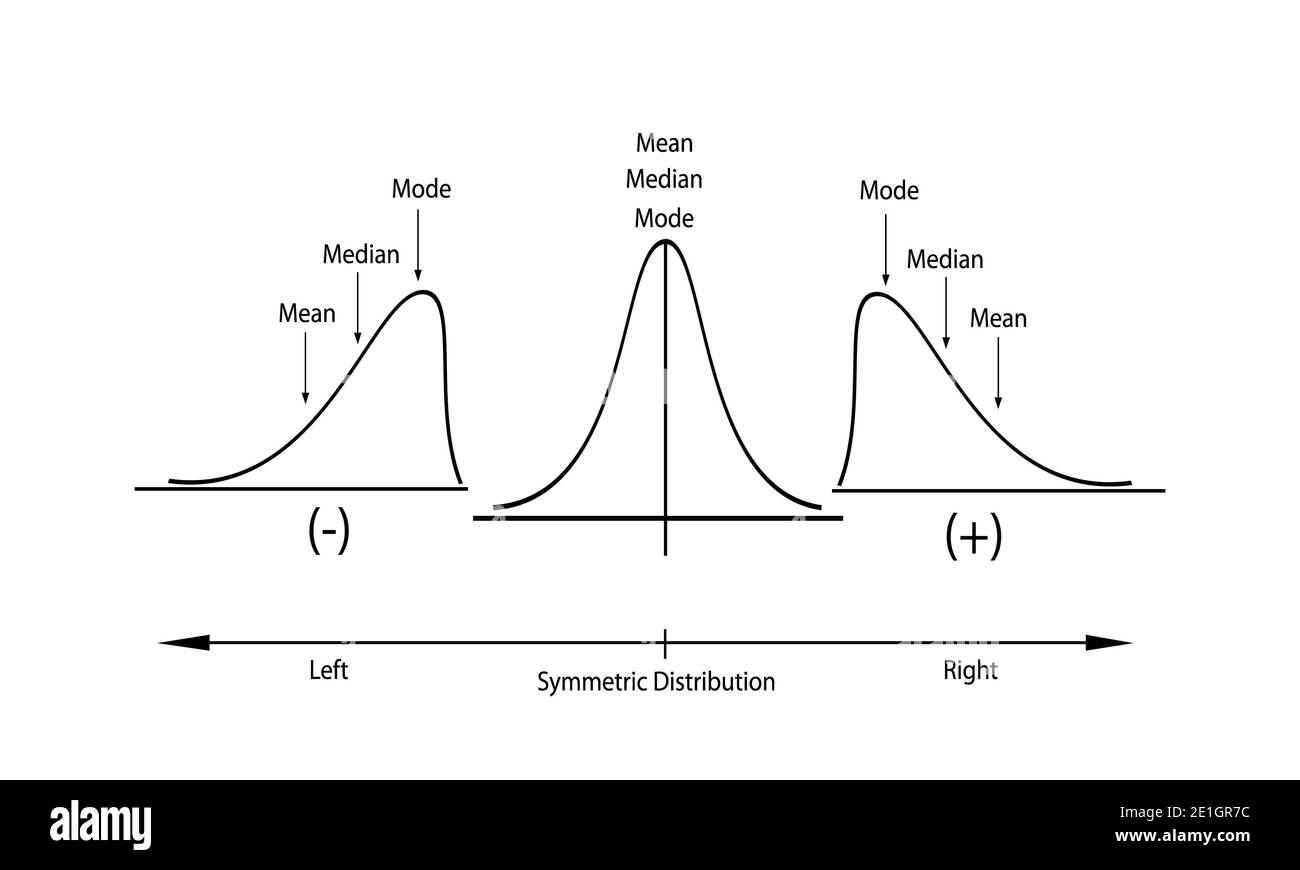
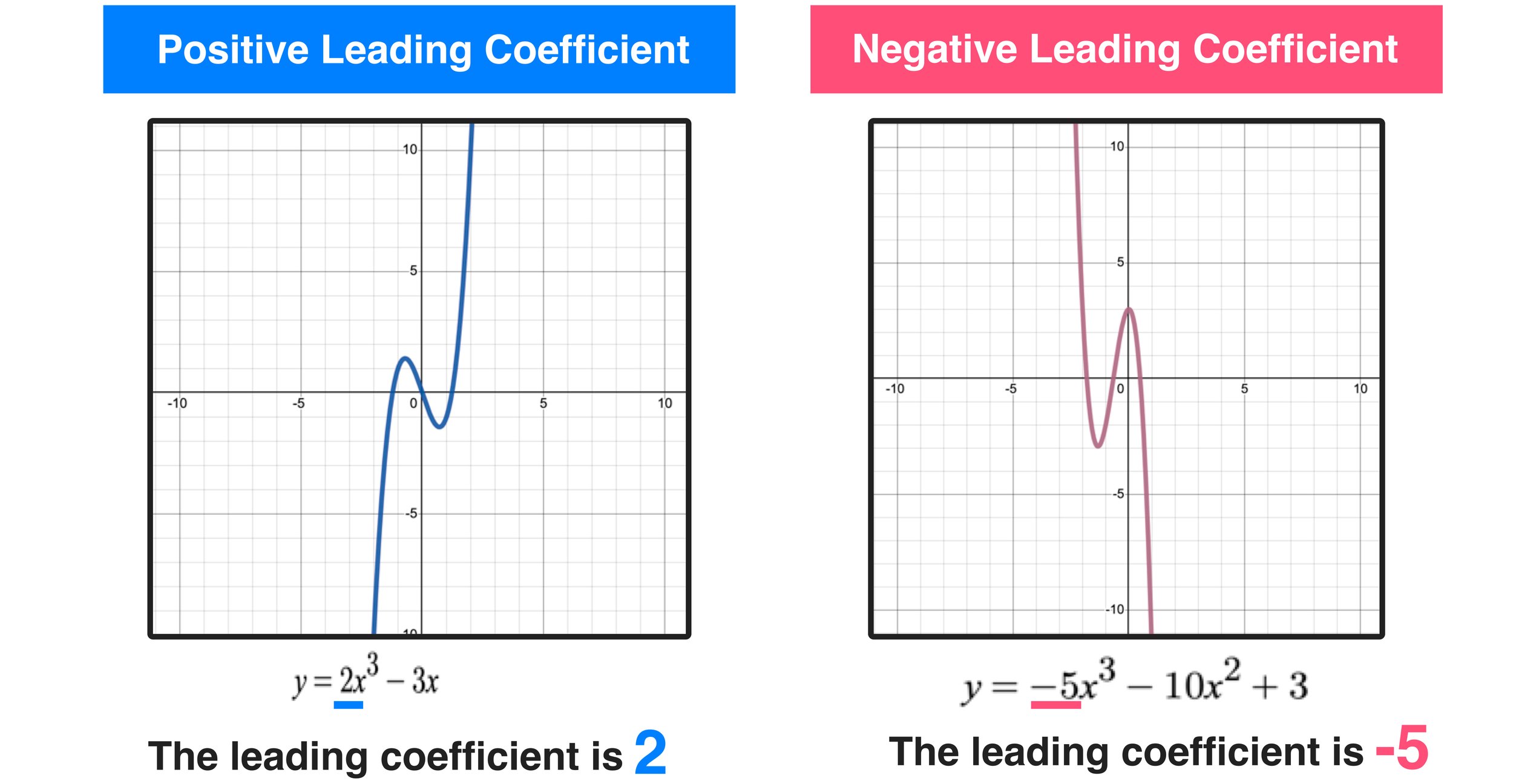
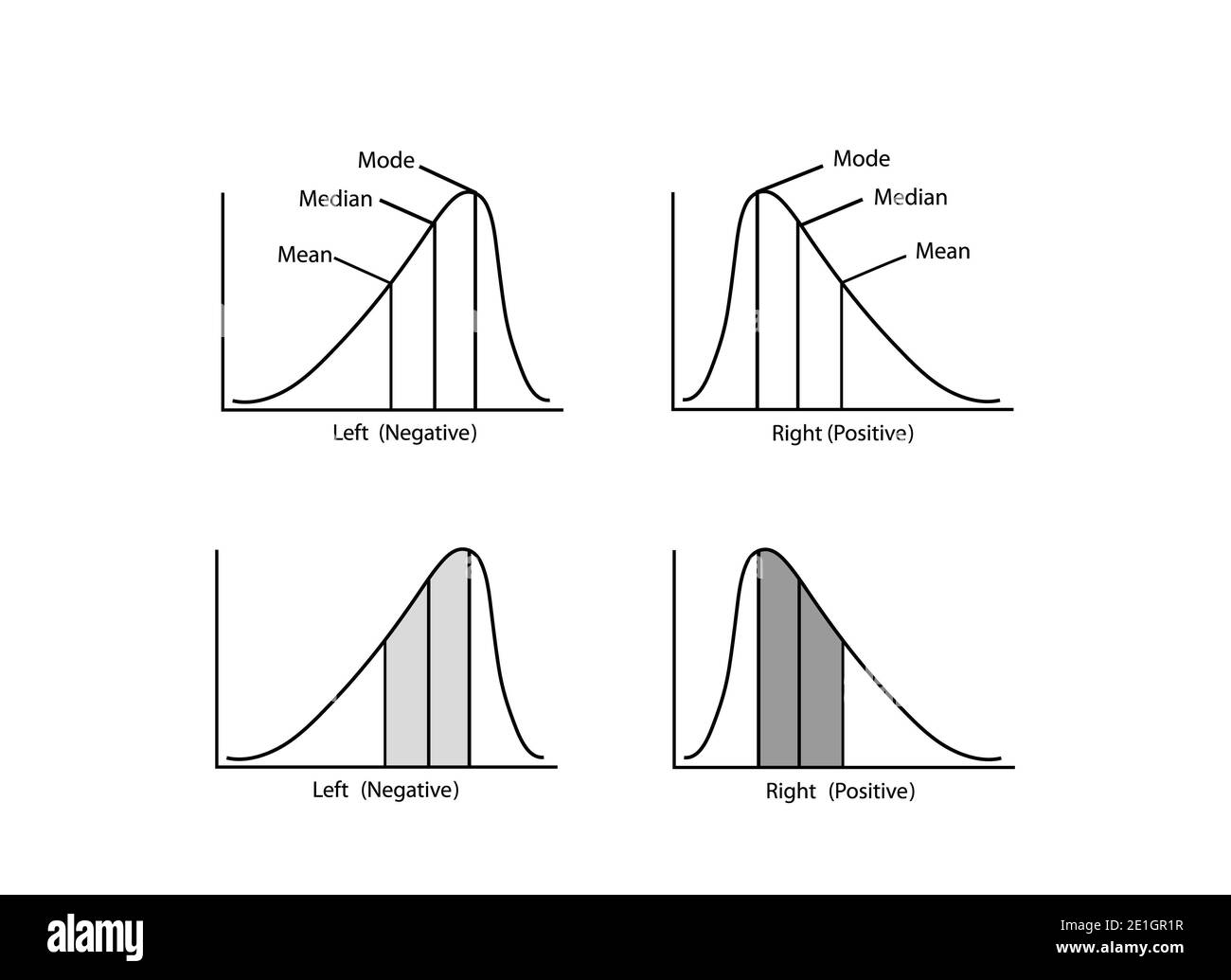
The function f(x) has a local maximum at critical points where the f 0 (x) changes from positive to The difference between positive and negative slope is what happens to y as x changes: Up is positive, and down is negative

The intuition behind the positive slope of lm is as follows: In the same way that: The slope of the curve is negative at.

Cutting the piece of sphere radially will help it fit (but not quite) over the flat piece of paper, but where the cut was made an angle will now form. Its derivative is 2x (see derivative rules) 2x continually increases, so the. Gradient of a slope positive and negative gradients.

Line, indicate where the derivative is positive and where it is negative. Negative slopes are based on as x increases, y is decreasing, so we end up with a negative change in y/positive change in x which gives a. We make scatterplots to see relationships between variables.

When the second derivative is negative, the function is concave downward. (alternatively, y decreases as x decreases.). It is positive if ${\bf t}$ turns counterclockwise, and negative if ${\bf t}$ turns clockwise when $s$ increases.

Positive slopes are based on as x increases, y is also increasing, so change in y/change in x is positive. At which points is the slope of the curve negative? Gradients can be calculated by dividing the vertical height by the horizontal.